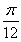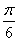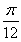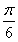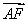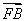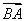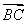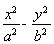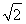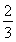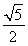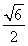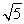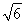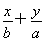题目内容
已知F1, F2是椭圆x2＋2y2＝6的两个焦点，点M在此椭圆上且∠F1MF2＝60°，则△MF1F2的面积等于( )
A.
B.
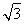C．2 D.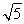
B
【解析】x2＋2y2＝6，即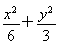
＝1，所以a＝
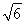，b＝c＝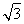
.设|MF1|＝t，则在△MF1F2中，由余弦定理得(2c)2＝(2a－t)2＋t2－2t(2a－t)cos 60°，解得t＝
±
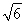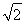，S△MF1F2＝
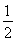|MF1||MF2|sin 60°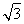＝，即△MF1F2的面积为.
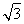练习册系列答案
相关题目
