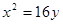题目内容
设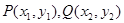 是抛物线
是抛物线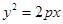
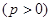 上相异两点,
上相异两点,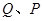 到y轴的距离的积为
到y轴的距离的积为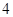 且
且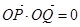 .
.
(1)求该抛物线的标准方程.
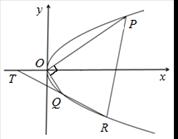
(2)过Q的直线与抛物线的另一交点为R,与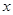 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
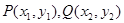 是抛物线
是抛物线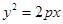
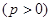 上相异两点,
上相异两点,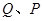 到y轴的距离的积为
到y轴的距离的积为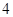 且
且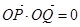 .
.
(1)求该抛物线的标准方程.
(2)过Q的直线与抛物线的另一交点为R,与
 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.(1) .(2)直线PQ垂直于x轴时|PR|取最小值
.(2)直线PQ垂直于x轴时|PR|取最小值 .
.
 .(2)直线PQ垂直于x轴时|PR|取最小值
.(2)直线PQ垂直于x轴时|PR|取最小值 .
.试题分析:(1)确定抛物线的标准方程,关键是确定
 的值.利用
的值.利用 ,可得
,可得 ,
,再根据P、Q在抛物线上,得到
 ,集合已知条件
,集合已知条件 ,得4p2=4,p=1.
,得4p2=4,p=1.(2)设直线PQ过点
 ,且方程为
,且方程为 ,应用联立方程组
,应用联立方程组
消去x得y2 2my 2a=0,利用韦达定理,建立
 的方程组,确定
的方程组,确定 得到
得到 ,利用“弦长公式”求解.
,利用“弦长公式”求解.试题解析: (1)∵ ·=0,则x1x2+y1y2=0, 1分
又P、Q在抛物线上,故y12=2px1,y22=2px2,故得
+y1y2=0, y1y2= 4p2
 3分
3分又|x1x2|=4,故得4p2=4,p=1.
所以抛物线的方程为:
 5分
5分(2)设直线PQ过点E(a,0)且方程为x=my+a
联立方程组

消去x得y2 2my 2a=0
∴
 ① 7分
① 7分设直线PR与x轴交于点M(b,0),则可设直线PR方程为x=ny+b,并设R(x3,y3),
同理可知
 ② 9分
② 9分由①、②可得

由题意,Q为线段RT的中点,∴ y3=2y2,∴b=2a
又由(Ⅰ)知, y1y2= 4,代入①,可得
2a= 4 ∴ a=2.故b=4. 11分
∴

∴

 .
.当n=0,即直线PQ垂直于x轴时|PR|取最小值
 14分
14分
练习册系列答案
相关题目
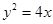 的焦点为F
的焦点为F 过点
过点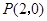 的直线交抛物线于A
的直线交抛物线于A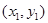 ,B
,B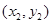 两点,直线AF,BF分别与抛物线交于点M,N
两点,直线AF,BF分别与抛物线交于点M,N 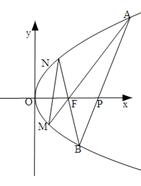
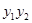 的值;
的值;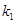 ,直线AB的斜率为
,直线AB的斜率为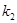 证明:
证明: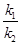 为定值
为定值 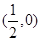 的距离比它到
的距离比它到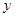 轴的距离大
轴的距离大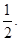
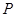 的轨迹
的轨迹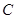 的方程;
的方程;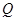 为曲线
为曲线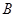 ,
,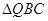 为圆
为圆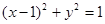 的外切三角形,求
的外切三角形,求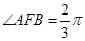 ,弦AB中点M在准线l上的射影为
,弦AB中点M在准线l上的射影为 ,则
,则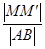 的最大值为( )
的最大值为( )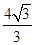
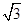
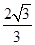
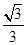
 的准线截圆
的准线截圆 所得弦长为2,则
所得弦长为2,则 = .
= .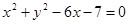 与抛物线
与抛物线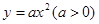 的准线相切,则
的准线相切,则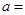 .
.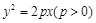 的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若
的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若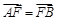 ,
,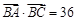 ,则抛物线的方程为 .
,则抛物线的方程为 . 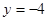 ,则抛物线的标准方程为( )
,则抛物线的标准方程为( )