题目内容
如图，平面AC⊥平面AE，且四边形ABCD与四边形ABEF都是正方形，则异面直线AC与BF所成角的大小是______．
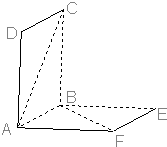
以A为坐标原点，AF，AB，AD方向分别为X，Y，Z轴正方向建立空间坐标系
设正方形ABCD与正方形ABEF的边长均为1
则A（0，0，0），B（0，1，0），C（0，1，1），F（1，0，0）
则
=（0，1，1），
=（1，-1，0）
设异面直线AC与BF所成角为θ，
则cosθ=|
|=
∴θ=60°
故答案为：60°
设正方形ABCD与正方形ABEF的边长均为1
则A（0，0，0），B（0，1，0），C（0，1，1），F（1，0，0）
则
| AC |
| BF |
设异面直线AC与BF所成角为θ，
则cosθ=|
| ||||
|
|
| 1 |
| 2 |
∴θ=60°
故答案为：60°
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
