题目内容
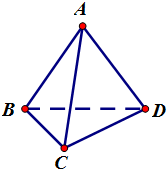
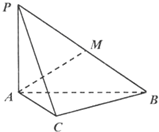
已知正四面体ABCD的棱长为a，点O是△BCD的中心，点M是CD中点．
（1）求点A到面BCD的距离；
（2）求AB与面BCD所成角的正弦值．
（1）求点A到面BCD的距离；
（2）求AB与面BCD所成角的正弦值．
（1）∵棱长为a的正四面体中
AB=BC=CD=BD=AC=AD=a
在等边三角形BCD中，CD边的上高BM=
a
过A作底面BCD上的高，则垂足O为底面BCD的重心
则BO=
BM=
a
则AO=
=
a，
∴点A到面BCD的距离OA=
a
（说明：直接由公式计算得出正确结果不扣分）…6分
（2）由（1）可得∠ABO即为AB与面BCD所成角
在Rt△OAB中，OA=
a，AB=a
∴sin∠ABO=
=
即AB与面BCD所成角的正弦值为
AB=BC=CD=BD=AC=AD=a
在等边三角形BCD中，CD边的上高BM=
| ||
| 2 |
过A作底面BCD上的高，则垂足O为底面BCD的重心
则BO=
| 2 |
| 3 |
| ||
| 3 |
则AO=
| AB2-BO2 |
| ||
| 3 |
∴点A到面BCD的距离OA=
| ||
| 3 |
（说明：直接由公式计算得出正确结果不扣分）…6分
（2）由（1）可得∠ABO即为AB与面BCD所成角
在Rt△OAB中，OA=
| ||
| 3 |
∴sin∠ABO=
| OA |
| AB |
| ||
| 3 |
即AB与面BCD所成角的正弦值为
| ||
| 3 |
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
