题目内容
【题目】已知数列an的首项a1=2，且an=2an﹣1﹣1（nN+ ， n≥2）．
（1）求数列{an}的通项公式；
（2）求数列{nan﹣n}的前n项和Sn ．
【答案】
（1）解：∵an=2an﹣1﹣1，
∴an﹣1=2（an﹣1﹣1），
即{an﹣1}是以a1﹣1=2﹣1=1，为首项，公比q=2的等比数列，
∴an﹣1=2n﹣1，即an=1+2n﹣1
（2）解：∵an=1+2n﹣1．，
∴nan﹣n=n（1+2n﹣1）﹣n=n2n﹣1，
数列{nan﹣n}的前n项和Sn=120+221+322+…+n2n﹣1，①
2Sn=121+222+323+…+（n﹣1）2n﹣1+n2n，②，
①﹣②得，﹣Sn=120+21+22+…+2n﹣1﹣n2n= 
﹣n2n=2n﹣n2n﹣1=（1﹣n）2n﹣1，
即Sn=（n﹣1）2n+1
【解析】（1）根据条件构造一个等比数列，即可求数列{an}的通项公式；（2）求出数列{nan﹣n}的通项公式，利用错位相减法即可求出前n项和Sn ．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系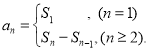
)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．
练习册系列答案
阅读快车系列答案
相关题目
