题目内容
【题目】化简求值：
（1）（1+tan2θ）cos2θ
（2）已知 
，求2+sinθcosθ﹣cos2θ的值．
【答案】
（1）解：（1+tan2θ）cos2θ
原式= 
=sin2θ+cos2θ=1
（2）解：法一：∵ 
，
∴sinθ= 
cosθ，
由sin2θ+cos2θ=1．
可得： 
，
∴cos2θ= 
那么：2+sinθcosθ﹣cos2θ=2﹣ 
cos2θ﹣cos2θ=2﹣ 
=2﹣ 
= 
．
法二：由2+sinθcosθ﹣cos2θ= 
= 
∵ ，
∴ = 
=
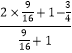故得 ，则2+sinθcosθ﹣cos2θ的值为 ．
【解析】（1）利用“切化弦”的思想求解．（2）利用“切化弦”的思想，在结合同角三角函数关系式求解．
练习册系列答案
相关题目
