题目内容
10.已知x,y∈R+,且x+2y=$\sqrt{3}$,则$\frac{xy+1}{{x}^{2}+4{y}^{2}}$的最大值为( )| A. | $\frac{11}{12}$ | B. | $\frac{11}{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 $\frac{xy+1}{{x}^{2}+4{y}^{2}}$=$\frac{xy+1}{(x+2y)^{2}-4xy}$=$\frac{xy+1}{3-4xy}$.利用基本不等式确定0<xy≤$\frac{3}{8}$,再换元,利用单调性,即可得出结论.
解答 解:$\frac{xy+1}{{x}^{2}+4{y}^{2}}$=$\frac{xy+1}{(x+2y)^{2}-4xy}$=$\frac{xy+1}{3-4xy}$.
∵x,y∈R+,且x+2y=$\sqrt{3}$,
∴$\sqrt{3}$=x+2y≥2$\sqrt{2xy}$,
∴0<xy≤$\frac{3}{8}$.
设t=3-4xy,xy=$\frac{1}{4}$(3-t),$\frac{3}{2}$≤t<3,
∴f(t)=$\frac{7}{4t}$-$\frac{1}{4}$在$\frac{3}{2}$≤t<3为减函数,
∴原式最大值为$\frac{11}{12}$.
∴f(t)max=f($\frac{3}{2}$)=$\frac{11}{12}$
∴原式最大值为$\frac{11}{12}$.
点评 本题考查求最大值,考查基本不等式的运用,考查函数的单调性,正确转化是关键.

练习册系列答案
相关题目
10.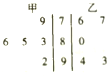 将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
①甲生的平均成绩大于乙生的平均成绩;
②甲生的平均成绩小于乙生的平均成绩;
③甲生成绩的方差大于乙生成绩的方差;
④甲生成绩的方差小于乙生成绩的方差.
其中根据茎叶图能得到正确的统计结论的编号为( )
 将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:①甲生的平均成绩大于乙生的平均成绩;
②甲生的平均成绩小于乙生的平均成绩;
③甲生成绩的方差大于乙生成绩的方差;
④甲生成绩的方差小于乙生成绩的方差.
其中根据茎叶图能得到正确的统计结论的编号为( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
2.函数f(x)=lg($\frac{1}{\sqrt{{x}^{2}+1}+x}$)的奇偶性是( )
| A. | 奇函数 | B. | 偶函数 | C. | 既奇又偶函数 | D. | 非奇非偶函数 |
19.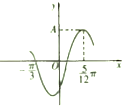 函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)的周期为( )
函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)的周期为( )
 函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)的周期为( )
函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)的周期为( )| A. | $\frac{π}{2}$ | B. | $\frac{3}{4}π$ | C. | π | D. | 2π |