题目内容
20.海滨城市威海附近有一台风,台风中心位于城市南偏东30°,距城市300km的海面P处,并以20km/h的速度向北偏西45°方向移动,如果侵袭的范围半径为120km圆形区域,几小时后该城市开始受到台风的侵袭(精确到0.1h)分析 当城市距离台风中心小于等于120km时,城市开始受到台风侵袭,所以只要城市距离台风移动方向大于等于120km即可;由题意,画出图形敏捷三角形.
解答 解:由题意如图,设台风中心x小时到达Q,开始侵袭城市,在△OQP中,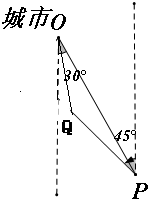
OQ=120km,OP=300km,∠OPQ=15°,PQ=20x,∠POQ=180°-15°-∠Q=165°-∠Q,
由正弦定理得到$\frac{300}{sinQ}=\frac{120}{sin15°}$=$\frac{20x}{sin∠POQ}$,
所以∠Q=40.3°(舍去)∠Q=139.7°,
所以∠A=25.3°,x=9.9(h)
所以大约9.9小时后该城市会受到台风的侵袭.
点评 本题主要考查了解三角形的实际应用;关键是由题意将问题转化为解三角形的问题.

练习册系列答案
相关题目