Question

【题目】某运输队接到给灾区运送物资的任务，该运输队有8辆载重为的型卡车，6辆载重为的型卡车，10名驾驶员，要求此运输队每天至少运送救灾物资．已知每辆卡车每天往返的次数为型卡车16次， 型卡车12次．每辆卡车每天往返的成本为型卡车240元， 型卡车378元．问每天派出型卡车与型卡车各多少辆，运输队所花的成本最低？

Answer 1

【答案】每天只派8辆型卡车运输，所花成本最低，最低成本为1920元．

【解析】试题分析： 先列表分析各限制条件：每天至少运送救灾物资，8辆载重为的型卡车，6辆载重为的型卡车，10名驾驶员，注意实际意义条件限制：卡车辆数为自然数，再根据限制条件画出可行域，根据目标函数（直线）平移得到最值取法.

试题解析：设每天派出型卡车辆， 型卡车辆，运输队所花成本为元，

则．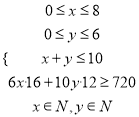

化简得，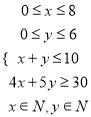

目标函数．

画出满足条件的可行域如图中阴影部分所示．

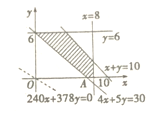
由图可知，当直线经过点时，截距最小，解方程组，

得点的坐标为，而问题中， ，故点不是最优解．

因此在可行域的整点中，点使取得最小值，即．

故每天只派8辆型卡车运输，所花成本最低，最低成本为1920元．