题目内容
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
【答案】(1) 详见解析(2) 详见解析(3) 60°.
【解析】
试题分析:(1) 证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要结合平几知识,如三角形中位线性质(2) 证明线面垂直,一般利用线面垂直判定与性质定理,经多次转化给予证明,其中线线垂直的寻找不仅可根据线面垂直关系转化,也可根据平几相关知识进行论证,如等腰三角形底边中线垂直于底边,正方形对角线相互垂直等(3) 先根据二面角定义确定平面角:∠EFD是二面角C-PB-D的平面角.再根据解对应三角形求角.
试题解析:
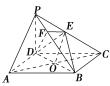
(1)证明 如图所示,
连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,
∴点O是AC的中点.
在△PAC中,EO是中位线,
∴PA∥EO.
而EO平面EDB且PA平面EDB,
∴PA∥平面EDB.
(2)证明 ∵PD⊥底面ABCD,且DC底面ABCD,
∴PD⊥DC.∵PD=DC,可知△PDC是等腰直角三角形.
而DE是斜边PC的中线,∴DE⊥PC.①
同样,由PD⊥底面ABCD,BC平面ABCD,
得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC.又PD∩CD=D,
∴BC⊥平面PDC.
而DE平面PDC,∴BC⊥DE.②
由①和②且PC∩BC=C可推得DE⊥平面PBC.
而PB平面PBC,∴DE⊥PB.
又EF⊥PB且DE∩EF=E,
∴PB⊥平面EFD.
(3)解 由(2)知,PB⊥DF.
故∠EFD是二面角C-PB-D的平面角.
由(2)知DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,
则PD=DC=a,BD=![]() a,
a,
PB=![]() a,PC=
a,PC=![]() a,DE=
a,DE=![]() a,
a,
在Rt△PDB中,DF=![]() a.
a.
在Rt△EFD中,sin∠EFD=![]() ,
,
∴∠EFD=60°.
∴二面角C-PB-D的大小为60°.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案