题目内容
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,长轴长为4.过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
,长轴长为4.过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.

(1)若直线l的斜率为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
【答案】(1)![]() (2)0<λ<1.
(2)0<λ<1.
【解析】试题分析:
首先求得椭圆方程为![]() ,圆的方程为
,圆的方程为![]() .
.
(1)法一:直线方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() ,则
,则![]() ,结合圆的性质可得
,结合圆的性质可得![]() ,则
,则![]() .
.
法二:联立直线方程与椭圆方程可得: ![]() ,则
,则![]() .
.
(2)由题意可得![]() ,设直线l:y=k(x+2),与椭圆方程联立可得
,设直线l:y=k(x+2),与椭圆方程联立可得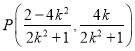 ,据此可得:
,据此可得: ![]() ,同理可得
,同理可得![]() ,则
,则![]() .
.
试题解析:
由题意得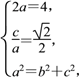 解得
解得![]()
所以椭圆的方程为![]() +
+![]() =1,圆的方程为x2+y2=4.
=1,圆的方程为x2+y2=4.
(1)法一 直线l的方程为y=![]() (x+2),
(x+2),
由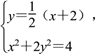 得3x3+4x-4=0.
得3x3+4x-4=0.
解得xA=-2,xP=![]() ,所以P
,所以P![]() .
.
所以AP=![]() =
=![]() .
.
又因为原点O到直线l的距离d=![]() =
=![]() ,
,
所以AQ=2![]() =
=![]() ,所以
,所以![]() =
=![]() =
=![]() .
.
法二 由![]() 得3y2-4y=0,所以yP=
得3y2-4y=0,所以yP=![]() .
.
由![]() 得5y2-8y=0,所以yQ=
得5y2-8y=0,所以yQ=![]() .
.
所以![]() =
=![]() =
=![]() ×
×![]() =
=![]() .
.
(2)若![]() =λ
=λ![]() ,则λ=
,则λ=![]() -1,
-1,
设直线l:y=k(x+2),
由![]() 得(2k2+1)x2+8k2x+8k2-4=0,
得(2k2+1)x2+8k2x+8k2-4=0,
即(x+2)[(2k2+1)x+(4k2-2)]=0,
所以xA=-2,xP=![]() ,得P
,得P![]() .
.
所以AP2=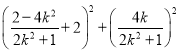 =
=![]() ,
,
即AP=![]() .同理可得AQ=
.同理可得AQ=![]() .
.
所以λ=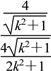 -1=1-
-1=1-![]() .
.
由题意知k2>0,所以0<λ<1.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目


