题目内容
【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
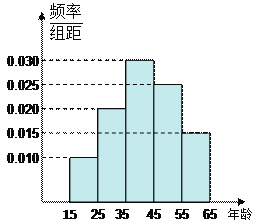
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
【答案】(1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(2) 第2组2人,第3组3人,第4组1人;(3)
;(2) 第2组2人,第3组3人,第4组1人;(3) ![]() .
.
【解析】试题分析:(1)观察表格,从第, ![]() 组频数为
组频数为![]() ,频率为
,频率为![]() 可知,所以第四组
可知,所以第四组![]() 人,而由频率分布直方图可知,第四组的频率为
人,而由频率分布直方图可知,第四组的频率为![]() ,所以总人数
,所以总人数![]() 人,根据频率分布直方图可知,第
人,根据频率分布直方图可知,第![]() 组频率分别为
组频率分别为![]() ,所以这四组的人数分别为
,所以这四组的人数分别为![]() 人,则可以分别计算得到
人,则可以分别计算得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(2)根据第(1)问可知,第
;(2)根据第(1)问可知,第![]() 组回答正确人数之比为
组回答正确人数之比为![]() ,所以若按分层抽样方法从这三组中抽取
,所以若按分层抽样方法从这三组中抽取![]() 人,应从
人,应从![]() 中分别抽出
中分别抽出![]() 人,
人, ![]() 人,
人, ![]() 人;(3)设第
人;(3)设第![]() 组两人为
组两人为![]() ,第
,第![]() 组三人为
组三人为![]() ,第
,第![]() 组一人为
组一人为![]() ,则从
,则从![]() 人中任意抽取
人中任意抽取![]() 人工包含
人工包含![]() 个基本事件,其中恰好没有第
个基本事件,其中恰好没有第![]() 组人共包含
组人共包含![]() 个基本事件,所以根据古典概型概率公式有
个基本事件,所以根据古典概型概率公式有![]() .
.
试题解析:(1)由频率表中第4组数据可知,第4组总人数为![]() ,
,
再结合频率分布直方图可知![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
(2)因为第2,3,4组回答正确的人数共有54人,
所以利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组:![]() 人;第3组:
人;第3组:![]() 人;第4组:
人;第4组:![]() 人
人
(3)设第2组2人为:A1,A2;第3组3人为:B1,B2,B3;第4组1人为:C1.
则从6人中随机抽取2人的所有可能的结果为:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2, B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1)
共15个基本事件
其中恰好没有第3组人共3个基本事件(A1,A2),(A2,C1),(A1,C1),
∴所抽取的人中恰好没有第3组人的概率是:![]() .
.

【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.