题目内容
【题目】如图所示,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,得
,得![]() ,所以
,所以![]() 平面
平面![]() ,取
,取![]() 中点
中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,写出各点坐标,求出
,写出各点坐标,求出![]() ,
,![]() ,
,![]() ,利用向量证得
,利用向量证得![]() ,
,![]() ,从而得到
,从而得到![]() ⊥平面
⊥平面![]() ;(2)先求出平面
;(2)先求出平面![]() 的法向量
的法向量![]() ,由(1)知
,由(1)知![]() 为平面
为平面![]() 的法向量,计算
的法向量,计算![]() ,然后可求出答案.
,然后可求出答案.
(1)取![]() 中点
中点![]() ,连结
,连结![]() .
.
∵![]() 为正三角形,∴
为正三角形,∴![]() .
.
∵在正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,如图所示,
,如图所示,
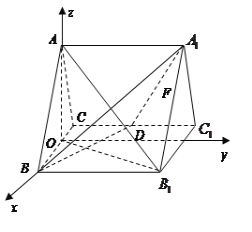
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,且
,且![]()
∴![]() 平面
平面![]() .
.
(2)设平面![]() 的法向量为
的法向量为![]() .
.![]() ,
,![]() .
.
∴ ,即
,即![]() ,解得
,解得![]() ,
,
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
由(1)知![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 的法向量,
的法向量,
∴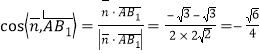 .
.
∴锐二面角![]() 的大小的余弦值为
的大小的余弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】共享单车是指企业在校园、地铁站点、公共站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,是共享经济的一种新形态.某共享单车企业在![]() 城市就“一天中一辆单车的平均成本与租用单车数量之间的关系”进行了调查,并将相关数据统计如下表:
城市就“一天中一辆单车的平均成本与租用单车数量之间的关系”进行了调查,并将相关数据统计如下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
根据以上数据,研究人员设计了两种不同的回归分析模型,得到两个拟合函数:
模型甲: ![]() ,模型乙:
,模型乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1元)(备注: ![]() ,
, ![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | 2.4 | 2 | 1.8 | 1.4 | |
残差 | 0 | 0 | 0.1 | 0.1 | ||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
, ![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这家企业在![]() 城市投放共享单车后,受到广大市民的热烈欢迎并供不应求,于是该企业决定增加单车投放量.根据市场调查,市场投放量达到1万辆时,平均每辆单车一天能收入7.2元;市场投放量达到1.2万辆时,平均每辆单车一天能收入6.8元.若按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,问该企业投放量选择1万辆还是1.2万辆能获得更多利润?请说明理由.(利润=收入-成本)
城市投放共享单车后,受到广大市民的热烈欢迎并供不应求,于是该企业决定增加单车投放量.根据市场调查,市场投放量达到1万辆时,平均每辆单车一天能收入7.2元;市场投放量达到1.2万辆时,平均每辆单车一天能收入6.8元.若按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,问该企业投放量选择1万辆还是1.2万辆能获得更多利润?请说明理由.(利润=收入-成本)
【题目】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | x | 1 |
B | 36 | y |
C | 54 | 3 |
(1)求x、y;
(2)若从高校B相关的人中选2人作专题发言,应采用什么抽样法,请写出合理的抽样过程.
【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
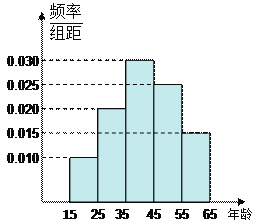
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.