题目内容
【题目】如图,在四棱锥A-EFCB中,![]() 为等边三角形,平面AEF
为等边三角形,平面AEF![]() 平面EFCB,
平面EFCB,![]() ,
,![]() ,
,![]() ,
,![]() ,O为EF的中点.
,O为EF的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角F-AE-B的余弦值;
(Ⅲ)若BE![]() 平面AOC,求a的值.
平面AOC,求a的值.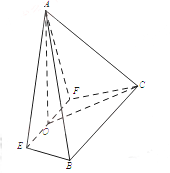
【答案】(I)证明见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】
(I)由于平面AEF![]() 平面EFCB,
平面EFCB,![]() 为等边三角形,O为EF的中点,则
为等边三角形,O为EF的中点,则![]() ,根据面面垂直性质定理,所以AO
,根据面面垂直性质定理,所以AO![]() 平面EFCB,又
平面EFCB,又![]() 平面EFCB,则
平面EFCB,则![]() .
.
(II) 取CB的中点D,链接OD,以O为原点,分别以OE,OD,OA为x,y,z轴建立空间直角坐标系,A![]() ,E
,E![]() ,B
,B![]() ,
,![]()
![]() ,
,![]() ,由于平面AEF与Y轴垂直,则设平面AEF的法向量为
,由于平面AEF与Y轴垂直,则设平面AEF的法向量为![]() ,设平面AEB的法向量
,设平面AEB的法向量![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,y=-1,则
,y=-1,则![]() ,二面角F-AE-B的余弦值cos(
,二面角F-AE-B的余弦值cos(![]() ,
,![]() )=
)=![]() =
=![]() ,由二面角F-AE-B为钝二面角,所以二面角F-AE-B的余弦值为
,由二面角F-AE-B为钝二面角,所以二面角F-AE-B的余弦值为![]() .
.
(Ⅲ)由(I)知![]() 平面EFCB,则
平面EFCB,则![]() ,若
,若![]() 平面
平面![]() ,只需
,只需![]() ,
,![]() ,又
,又![]() ,
,![]() ,解得
,解得![]() 或
或![]() ,由于
,由于![]() ,则
,则![]() .
.
【考点精析】利用向量语言表述线线的垂直、平行关系对题目进行判断即可得到答案,需要熟知设直线![]() 的方向向量分别是
的方向向量分别是![]() ,则要证明
,则要证明![]() ∥
∥![]() ,只需证明
,只需证明![]() ∥
∥![]() ,即
,即![]() ;则要证明
;则要证明![]() ,只需证明
,只需证明![]() ,即
,即![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目