题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)求![]() 的值域,设
的值域,设![]() ,
,![]() 为实数),求
为实数),求![]() 在
在![]() 时的最大值
时的最大值![]() ;
;
(3)对(2)中![]() ,若
,若![]() 对
对![]() 的所有实数
的所有实数![]() 及
及![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;
(2)![]() ,
,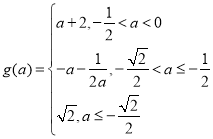 ;
;
(3)![]() 或
或![]() .
.
【解析】
(1)由![]() 且
且![]() 可求得定义域,可得
可求得定义域,可得![]() 的解析式;
的解析式;
(2)![]() ,令
,令![]() ,则
,则![]() ,由此可转化为关于
,由此可转化为关于![]() 的二次函数,按照对称轴
的二次函数,按照对称轴![]() 与
与![]() 的范围
的范围![]() ,
,![]() 的位置关系分三种情况讨论,借助单调性即可求得其最大值;
的位置关系分三种情况讨论,借助单调性即可求得其最大值;
(3)先由(2)求出函数![]() 的最小值,
的最小值,![]() 对
对![]() 恒成立,即要使
恒成立,即要使![]() 恒成立,从而转化为关于
恒成立,从而转化为关于![]() 的一次不等式,再根据一次函数的单调性可得不等式组,解出即可.
的一次不等式,再根据一次函数的单调性可得不等式组,解出即可.
(1)由![]() 且
且![]() ,得
,得![]() ,
,
所以函数的定义域为![]() .
.
又![]() ;
;
(2)![]()
![]() ,
,
由![]() ,且
,且![]() ,得
,得![]() .
.
令![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
由题意知![]() 即为函数
即为函数![]() ,
,![]() 的最大值.
的最大值.
注意到直线![]() 是抛物线
是抛物线![]() 的对称轴,
的对称轴,
因为![]() 时,函数
时,函数![]() ,
,![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
①若![]() ,即
,即![]() ,则
,则![]()
![]() ;
;
②若![]() ,即
,即![]() ,则
,则![]()
![]() ;
;
③若![]() ,即
,即![]() ,则
,则![]()
![]()
![]() ,
,
综上有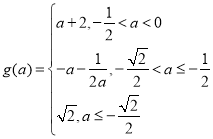 ;
;
(3)由![]() 的解析式可得
的解析式可得![]() 时,
时,![]()
![]() ,
,![]() ;
;
![]() 时,
时,![]()
![]() ;
;
可得![]()
![]() ,
,
由![]() 对
对![]() 恒成立,
恒成立,
即要使![]() 恒成立,
恒成立,
![]() ,令
,令![]() ,
,
对所有的![]() ,
,![]() 成立,
成立,
只需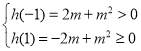 ,即有
,即有 ,
,
解得![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
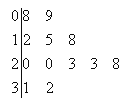
【题目】某单位附近只有甲,乙两个临时停车场,它们各有50个车位,为了方便市民停车,某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录,如下表:
时间 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
停车场甲 | 10 | 3 | 12 | 6 | 12 | 17 |
停车场乙 | 13 | 4 | 3 | 2 | 6 | 19 |
如果表中某一时刻停车场剩余停车位数低于总车位数的10%,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(Ⅰ)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(Ⅱ)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(Ⅲ)当停车场乙发出饱和警报时,求停车场甲也发出饱和警报的概率.