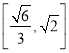题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() ,
,![]() 成等比数列,求直线
成等比数列,求直线![]() 的极坐标方程.
的极坐标方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)利用余弦的二倍角公式,结合极坐标与直角坐标转化公式进行求解即可;
(2)写出直线![]() 的参数方程,求出
的参数方程,求出![]() 的表达式,将直线
的表达式,将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程中,利用参数的意义,结合等比数列的性质进行求解即可.
的直角坐标方程中,利用参数的意义,结合等比数列的性质进行求解即可.
(1)方程![]() 可化为
可化为![]() ,
,
将![]() 代入上式,得曲线
代入上式,得曲线![]() 的直角坐标方程
的直角坐标方程![]() .
.
(2)由直线![]() 的方程为
的方程为![]() ,知直线
,知直线![]() 过点
过点![]() ,
,
记直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]() ,
,
设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
令![]() ,得点
,得点![]() 对应的参数值为
对应的参数值为![]() ,即
,即![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
整理,得![]() ,
,
则有![]() .
.
设![]() ,
,![]() 对应的参数值分别为
对应的参数值分别为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,
所以![]() ,
,
所以![]() 或
或![]() ,
,
解得![]() 或
或![]() ,
,
![]() 的普通方程为
的普通方程为![]() 或
或![]() ,
,
故![]() 的极坐标方程为
的极坐标方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?