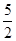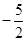题目内容
已知函数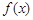 满足:①定义域为R;②
满足:①定义域为R;②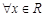 ,有
,有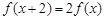 ;③当
;③当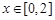 时,
时,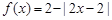 .记
.记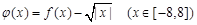 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数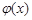 的零点个数为 ( )
的零点个数为 ( )
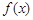 满足:①定义域为R;②
满足:①定义域为R;②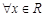 ,有
,有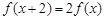 ;③当
;③当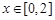 时,
时,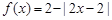 .记
.记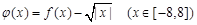 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数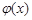 的零点个数为 ( )
的零点个数为 ( )| A.15 | B.10 | C.9 | D.8 |
B
根据条件:③当x∈[0,2]时,f(x)=2-|2x-2|可以作出函数图象位于[0,2]的拆线,再由?x∈R,有f(x+2)=2f(x),可将图象向右伸长,每向右两个单位长度,纵坐标变为原两倍,由此可以作出f(x)的图象,找出其与g(x)= 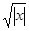 (x∈[-8,8])的交点,就可以得出φ(x)的零点,问题迎刃而解.
(x∈[-8,8])的交点,就可以得出φ(x)的零点,问题迎刃而解.
解:根据题意,作出函数y=f(x)(-8≤x≤8)的图象:
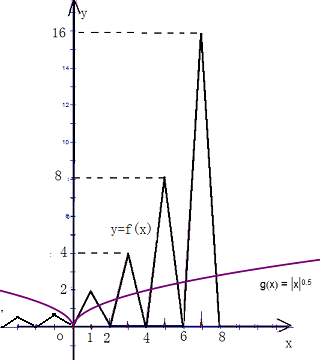
在同一坐标系里作出g(x)=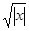 (x∈[-8,8])的图象,可得两图象在x轴右侧有8个交点.
(x∈[-8,8])的图象,可得两图象在x轴右侧有8个交点.
所以φ(x)="f(x)-"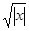 (x∈[-8,8])有8个零点,
(x∈[-8,8])有8个零点,
∵任意的x,有f(x+2)=2f(x),
∴当x=-1时,f(-1+2)=2f(-1)?f(-1)=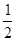 f(1)=1,满足φ(x)="f(x)-"
f(1)=1,满足φ(x)="f(x)-" 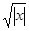 =0
=0
而x=0也是函数φ(x)的一个零点,并且当x<-1时,函数φ(x)没有零点
综上所述,函数φ(x)的零点一共10个
故选B
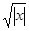 (x∈[-8,8])的交点,就可以得出φ(x)的零点,问题迎刃而解.
(x∈[-8,8])的交点,就可以得出φ(x)的零点,问题迎刃而解.解:根据题意,作出函数y=f(x)(-8≤x≤8)的图象:

在同一坐标系里作出g(x)=
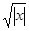 (x∈[-8,8])的图象,可得两图象在x轴右侧有8个交点.
(x∈[-8,8])的图象,可得两图象在x轴右侧有8个交点.所以φ(x)="f(x)-"
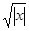 (x∈[-8,8])有8个零点,
(x∈[-8,8])有8个零点,∵任意的x,有f(x+2)=2f(x),
∴当x=-1时,f(-1+2)=2f(-1)?f(-1)=
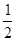 f(1)=1,满足φ(x)="f(x)-"
f(1)=1,满足φ(x)="f(x)-" 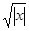 =0
=0而x=0也是函数φ(x)的一个零点,并且当x<-1时,函数φ(x)没有零点
综上所述,函数φ(x)的零点一共10个
故选B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 数
数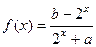 是奇函数
是奇函数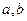 的值;
的值;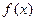 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;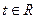 ,不等式
,不等式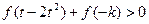 恒成立,求实数
恒成立,求实数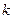 的取值范围。
的取值范围。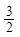 ,0)时,f(x)=log2(-3x+1),则f(2011)=( )
,0)时,f(x)=log2(-3x+1),则f(2011)=( )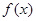 是
是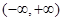 上的偶函数,若对于
上的偶函数,若对于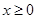 ,都有
,都有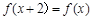 ,且当
,且当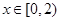 时,
时,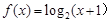 ,则
,则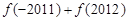 的值为
的值为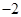
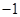
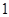
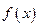 是定义在R上的奇函数,若
是定义在R上的奇函数,若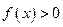 。则以下不等式不一定成立的是 ( )
。则以下不等式不一定成立的是 ( )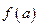 >
>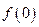
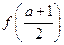 >
>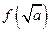
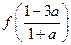 >
>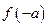
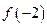
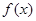 在
在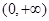 上是增函数,且
上是增函数,且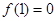 ,则不等式
,则不等式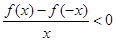
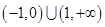
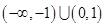
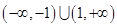
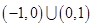
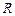 上的奇函数
上的奇函数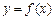 满足
满足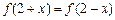 ,当
,当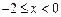 时,
时,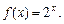 若
若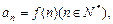 则
则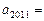 .
.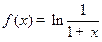 ,那么当xÎ(-1,0)时,f(x)=
,那么当xÎ(-1,0)时,f(x)= 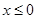 时
时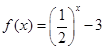 ,则
,则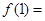 ( )
( )