题目内容
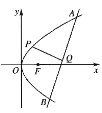
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线上一点,且
是抛物线上一点,且![]() ,直线
,直线![]() 过定点(4,0),与抛物线
过定点(4,0),与抛物线![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影是
上的射影是![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
(1)根据抛物线上的点到抛物线焦点的距离等于该点到抛物线准线的距离求解![]() 的值,进而根据点在抛物线上求解
的值,进而根据点在抛物线上求解![]() 的值;(2)联立直线与抛物线的方程得到一元二次方程,利用韦达定理结合两直线垂直或线段的长度的关系求解参数的值,进而确定直线方程.
的值;(2)联立直线与抛物线的方程得到一元二次方程,利用韦达定理结合两直线垂直或线段的长度的关系求解参数的值,进而确定直线方程.
解:(1)由![]() 得
得![]() ,所以
,所以![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() .
.
(2)解法一:因为![]() ,由(1)知点
,由(1)知点![]() ,
,
抛物线![]() 的方程为
的方程为![]() ,
,
设直线![]() 的方程是
的方程是![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
且![]() ,
,
由![]() ,
,
得![]() ,
,
即![]() ,
,
![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
所以直线![]() 的方程是
的方程是![]() ,
,
即![]() .
.
解法二:因为![]() ,由(1)知点
,由(1)知点![]() ,
,
抛物线![]() 的方程为
的方程为![]() ,
,
设直线![]() 的方程是
的方程是![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,
则![]() ,
,
由![]()
解得![]() 点的纵坐标是
点的纵坐标是![]() ,
,
![]() ,
,
![]()
![]() ,
,
因为![]() ,
,
所以![]()
 ,
,
化简得![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
所以直线![]() 的方程是
的方程是![]() ,
,
即![]()

 百年学典课时学练测系列答案
百年学典课时学练测系列答案【题目】为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在![]() 以及
以及![]() 的茎叶图,分别如图23所示.
的茎叶图,分别如图23所示.
成绩 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1

(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() “近似满足正态分布
“近似满足正态分布![]() 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取![]() 和
和![]() 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布![]() 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |
|
|
现在从不低于90同学中随机选一名同学,记其获奖金额为![]() ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:![]() )
)