Question

3．如图所示，定点A和B都在平面α内，顶点P∉α，PB⊥α，C是α内异于A和B的动点，且PC⊥AC，则BC与AC的位置关系是AC⊥BC．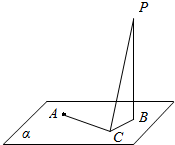

Answer 1

分析 通过证明AC⊥平面PBC，得出AC⊥BC，即可得出△ABC是直角三角形．

解答 解：∵A∈α，C∈α，∴AC?α；
又∵PB⊥α，∴PB⊥AC；
又∵PC⊥AC，
PB∩PC=B，
∴AC⊥平面PBC；
又∵BC?平面PBC，
∴AC⊥BC．
故答案为：AC⊥BC．

点评 本题考查了空间中的垂直关系的判断问题，解题时应明确线线垂直和线面垂直的判断与性质是什么，是中档题．