题目内容
18.在四面体ABCD中,AB=3,BC=7,CD=11,DA=9.则$\overrightarrow{AC}$•$\overrightarrow{BD}$的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
分析 可画出四面体ABCD,然后作DE⊥AC,垂足为E,并且连接BE,容易得出BC2-AB2=CD2-DA2=CE2-AE2,根据余弦定理可分别表示出BC2,AB2,从而可以得出2BE•AE•cos∠AEB-2BE•CE•cos∠BEC=0,进一步可得出cos∠BEC=0,从而得到AC⊥BE,这样由线面垂直的判定定理便可得出AC⊥平面BDE,从而得到AC⊥BD,这时便可得出$\overrightarrow{AC}•\overrightarrow{BD}$的值.
解答 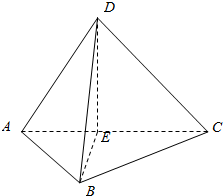 解:如图,过D作DE⊥AC,垂足为E,连接BE,则:
解:如图,过D作DE⊥AC,垂足为E,连接BE,则:
CD2=CE2+DE2,DA2=AE2+DE2;
∴DA2-CD2=CE2-AE2;
又BC2-AB2=DA2-CD2;
∴BC2-AB2=CE2-AE2;
BC2=BE2+CE2-2BE•CE•cos∠BEC,AB2=BE2+AE2-2BE•AE•cos∠AEB;
∴BC2-AB2=CE2-AE2+2BE•AE•cos∠AEB-2BE•CE•cos∠BEC=CE2-AE2;
∴2BE•AE•cos∠AEB-2BE•CE•cos∠BEC=0;
∴2BE•AE•cos∠AEB+2BE•CE•cos∠AEB=0;
即(2BE•AE+2BE•CE)cos∠AEB=0;
∴cos∠AEB=0;
∴∠AEB=90°;
即AC⊥BE,又AC⊥DE,BE∩DE=E;
∴AC⊥平面BDE;
∴AC⊥BD;
∴$\overrightarrow{AC}•\overrightarrow{BD}=0$.
故选A.
点评 考查直角三角形边的关系,以及余弦定理,已知三角函数求值,线面垂直的判定定理,向量垂直的充要条件.

练习册系列答案
相关题目
8.已知等比数列{an}满足a1=2,16a3a5=8a4-1,则a2=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
6.下面命题:①{1,2,3,4}是由四个元素组成的集合;②集合{0}表示仅有一个数“0”组成的集合;③集合{1,2,3}与{3,1,2}是同一个集合;④集合{小于1的正有理数}是一个有限集,其中正确的是( )
| A. | ①,②,③ | B. | ②,③,④ | C. | ③,④ | D. | ② |
10.已知函数y=sin(ωx+$\frac{π}{4}$)(ω>0)的最小正周期为$\frac{2π}{5}$,则ω等于( )
| A. | 5 | B. | 5π | C. | $\frac{4}{5}$ | D. | $\frac{5}{2}$ |
7.圆台轴截面的两条对角线互相垂直,上、下地面半径之比为3:4,高为14$\sqrt{2}$,则母线长为( )
| A. | 10$\sqrt{3}$ | B. | 25 | C. | 10$\sqrt{2}$ | D. | 20 |