题目内容
11.指出下列各组命题中,p是q的什么条件:(1)在△ABC中,p:A>B,q:sinA>sinB;
(2)p:|x+1|>2,q:(x-2)(x-3)<0.
分析 (1)由正弦定理知理 $\frac{a}{sinA}$=$\frac{b}{sinB}$=2R,sinA>sinB,知a>b,所以A>B,反之亦然,故可得结论.
(2)分别解不等式求出p,q的解集,再根据必要条件和充分条件判断即可.
解答 解:(1)解:若sinA>sinB成立,
由正弦定理 $\frac{a}{sinA}$=$\frac{b}{sinB}$=2R,
所以a>b,
所以A>B.
反之,若A>B成立,
所以a>b,
因为a=2RsinA,b=2RsinB,
所以sinA>sinB,
所以p是q的充要条件;
(2))p:|x+1|>2,
∴x+1>2,或x+1<-2,
∴x>1,或x<-3,
q:(x-2)(x-3)<0,
解得2<x<3,
∴q⇒p,但p不能推出q,
故p是q的必要不充分条件.
点评 本题以三角形和不等式为载体,考查四种条件,解题的关键是正确运用正弦定理及解不等式.属于基础题

练习册系列答案
相关题目
1.点M是抛物线y=$\frac{1}{4}$x2上一点,F为抛物线的焦点,以MF为直径的圆与x轴的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
19.函数f(x)=4x2-kx-8在区间(-∞,5]上是减函数,则实数k的取值范围是( )
| A. | k≥40 | B. | k≤40 | C. | k≥5 | D. | k≤5 |
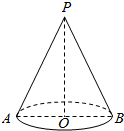 如图所示,圆锥的母线长l,轴截面PAB内,∠PAO=60°,
如图所示,圆锥的母线长l,轴截面PAB内,∠PAO=60°, 如图,圆心在原点,半径为R的圆交x轴正半轴于点A,P、Q是圆上的两个动点,它们同时从点A出发沿圆周做匀速运动.点P逆时针方向每秒转$\frac{π}{3}$,点Q顺时针方向每秒转$\frac{π}{6}$,试求它们出发后第五次相遇时的位置及各自走过的弧长.
如图,圆心在原点,半径为R的圆交x轴正半轴于点A,P、Q是圆上的两个动点,它们同时从点A出发沿圆周做匀速运动.点P逆时针方向每秒转$\frac{π}{3}$,点Q顺时针方向每秒转$\frac{π}{6}$,试求它们出发后第五次相遇时的位置及各自走过的弧长.