题目内容
【题目】将5个小球放到3个盒子中,在下列条件下,各有多少种投放方法?
①小球不同,盒子不同,盒子不空;
②小球不同,盒子不同,盒子可空;
③小球不同,盒子相同,盒子不空;
④小球不同,盒子相同,盒子可空;
⑤小球相同,盒子不同,盒子不空;
⑥小球相同,盒子不同,盒子可空;
⑦小球相同,盒子相同,盒子不空;
⑧小球相同,盒子相同.
【答案】解:①小球不同,盒子不同,盒子不空,将小球分成3份,每份1,1,3或1,2,2,再放在3个不同的盒子中,有 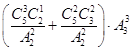 =150种;
=150种;
②小球不同,盒子不同,盒子可空,有35种;
③小球不同,盒子相同,盒子不空,将5个不同小球分成3份,分法为1,1,3;1,2,2,共有 ![]() =25种;
=25种;
④小球不同,盒子相同,盒子可空,将5个不同的小球分成1份、2份、3份,共有 ![]() +(
+( ![]() )+
)+ ![]() =41;
=41;
⑤小球相同,盒子不同,盒子不空,用隔板法,有 ![]() =6种方法;
=6种方法;
⑥小球相同,盒子不同,盒子可空,把5个小球及插入的2个隔板都设为小球,7个小球种任选两个变为隔板(可以相邻),那么2块隔板分成3份的小球数对应于相应的3个不同盒子,故有 ![]() =21种;
=21种;
⑦小球相同,盒子相同,盒子不空,5个相同的小球分成3份即可,有3,1,1;2,2,1,共2种;
⑧小球相同,盒子相同,只要将5个相同小球分成1份,2份,3份.分法如下:5,0,0;4,1,0;3,2,0;3,1,1;2,2,1,共5种
【解析】根据不同情况,利用先分后排的方法,即可得出结论.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目