题目内容
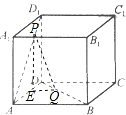
【题目】如图,正方体ABCD﹣A1B1C1D1棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12, 
(1)求线段PQ的长度;
(2)求证PQ⊥AD;
(3)求证:PQ∥平面CDD1C1 .
【答案】
(1)解:在AD上取点E,使得DE:EA=5:12,
∵D1P:PA=DQ:QB=5:12,
∴PE∥DD1,EQ∥AB,
∴PE⊥AD,EQ⊥AD
∵正方体ABCD﹣A1B1C1D1棱长为1,
∴PE= ![]() ,EQ=
,EQ= ![]() ,
,
∴PQ= ![]() =
= ![]()
(2)证明:∵PE⊥AD,EQ⊥AD,PE∩EQ=E,
∴AD⊥平面PEQ,
∵PQ平面PEQ,
∴PQ⊥AD
(3)证明:∵PE∥DD1,PE平面CDD1C1,DD1平面CDD1C1,
∴PE∥平面CDD1C1,
同理EQ∥平面CDD1C1,
∵PE∩EQ=E,
∴平面PEQ∥平面CDD1C1,
∵PQ平面PEQ,
∴PQ∥平面CDD1C1.
【解析】(1)在AD上取点E,使得DE:EA=5:12,可得PE= ![]() ,ED=
,ED= ![]() ,利用勾股定理,求出线段PQ的长度;(2)证明AD⊥平面PEQ,可得PQ⊥AD;(3)证明平面PEQ∥平面CDD1C1 , 可得PQ∥平面CDD1C1 .
,利用勾股定理,求出线段PQ的长度;(2)证明AD⊥平面PEQ,可得PQ⊥AD;(3)证明平面PEQ∥平面CDD1C1 , 可得PQ∥平面CDD1C1 .
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形,以及对空间中直线与直线之间的位置关系的理解,了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

练习册系列答案
相关题目