题目内容
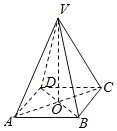
【题目】在正四棱锥![]() 中,底面正方形
中,底面正方形![]() 的边长为1,侧棱长为2,则异面直线
的边长为1,侧棱长为2,则异面直线![]() 与
与![]() 所成角的大小为__________.
所成角的大小为__________.

【答案】![]()
【解析】
连接AC,交BD于O,连接VO,可得对角线AC、BD互相垂直,再在三角形VBD中,根据VB=VD和O为BD中点,证出VO、BD互相垂直,最后根据直线与平面垂直的判定理证出BD⊥平面ACV,从而BD⊥VA,即异面直线VA与BD所成角大小.
如图所示,连接AC,交BD于O,连接VO
∵四边形ABCD是正方形,
∴AC⊥BD,O为BD的中点
又∵正四棱锥V﹣ABCD中,VB=VD
∴VO⊥BD
∵AC∩VO=O,AC、VO平面ACV
∴BD⊥平面ACV
∵VA平面ACV
∴BD⊥VA;
即异面直线VA与BD所成角等于![]() ..
..
故答案为![]() .
.

【题目】某商品每千克定价10元,商家采取了如下的促销方式:
一次购买量 | 促销方式 |
不多于20千克 | 原价出售 |
多于20千克且不多于40千克 | 不多于20千克部分,原价出售 多于20千克部分,九折出售 |
多于40千克 | 不多于20千克部分,原价出售 多于20千克且不多于40千克部分,九折出售 多于40千克部分八折出售 |
(1)求一次购买![]() (单位:千克),此商品的花费
(单位:千克),此商品的花费![]() (单位:元)的函数解析式;
(单位:元)的函数解析式;
(2)某人一次购买此商品400元,问他能购得此商品多少千克?
【题目】气象部门提供了某地区今年六月分(30天)的日最高气温的统计表如下:
日最高气温t(单位: |
|
|
|
|
天数 | 6 | 12 |
|
|
由于工作疏忽,统计表被墨水污染,![]() 和
和![]() 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于![]() 的频率为0.9.
的频率为0.9.
(1)若把频率看作概率,求![]() ,
,![]() 的值;
的值;
(2)把日最高气温高干![]() 称为本地区的“高温天气”,根据已知条件完成下面2×2列联表,并据此推测是否有95%的把握认为本地区“高温天气”与西瓜“旺销”有关?说明理由.
称为本地区的“高温天气”,根据已知条件完成下面2×2列联表,并据此推测是否有95%的把握认为本地区“高温天气”与西瓜“旺销”有关?说明理由.
高温天气 | 非高温天气 | 合计 | |
旺销 | 1 | ||
不旺销 | 6 | ||
合计 |
附![]()
P(K2≥R) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |