题目内容
如图,已知 为平行四边形,
为平行四边形, ,
, ,
, ,点
,点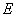 在
在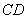 上,
上, ,
, ,
, 与
与 相交于
相交于 .现将四边形
.现将四边形 沿
沿 折起,使点
折起,使点 在平面
在平面 上的射影恰在直线
上的射影恰在直线 上.
上.

(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求折后直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
 为平行四边形,
为平行四边形, ,
, ,
, ,点
,点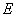 在
在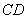 上,
上, ,
, ,
, 与
与 相交于
相交于 .现将四边形
.现将四边形 沿
沿 折起,使点
折起,使点 在平面
在平面 上的射影恰在直线
上的射影恰在直线 上.
上.
(Ⅰ) 求证:
 平面
平面 ;
;(Ⅱ) 求折后直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值.(1)要证明线面垂直,只要通过线线垂直来判定线面垂直即可。
(2)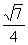
(2)
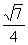
试题分析:解:(Ⅰ)∵EF⊥DN,EF⊥BN,DN∩BN=N
∴EF⊥面DNB ∵EF?平面BCEF,∴平面BDN⊥平面BCEF,∵BN=平面BDN∩平面BCEF,∴D在平面BCEF上的射影在直线BN上,∵D在平面BCEF上的射影在直线BC上,∴D在平面BCEF上的射影即为点B,∴BD⊥平面BCEF. 6分
(Ⅱ)连接BE,由BD⊥平面BCEF,得∠DEB即为直线DE与平面BCEF所成角.在原图中,由已知,可得AD=3,BD=3
 ,BN=
,BN= ,DN=2
,DN=2 ,DE=4 折后,由BD⊥平面BCEF,知BD⊥BN则BD2=DN2-BN2=9,即BD=3则在Rt△DEB中,有BD=3,DE=4,则BE=
,DE=4 折后,由BD⊥平面BCEF,知BD⊥BN则BD2=DN2-BN2=9,即BD=3则在Rt△DEB中,有BD=3,DE=4,则BE=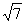 ,故cos∠DEB=
,故cos∠DEB=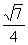 即折后直线DE与平面BCEF所成角的余弦值为
即折后直线DE与平面BCEF所成角的余弦值为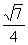 14分
14分点评:主要是考查了空间几何体中线面垂直的证明以及线面角的求解的综合运用,属于基础题。

练习册系列答案
相关题目
 和平面
和平面 ,有如下四个命题:
,有如下四个命题: ,则
,则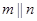 ;
;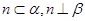 ,则
,则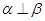 ;
;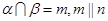 ,则
,则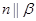 且
且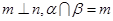 ,则
,则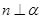 或
或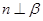 。其中真命题的个数是 .
。其中真命题的个数是 .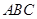 —
—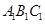 ,侧面
,侧面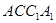 与底面
与底面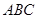 垂直,∠
垂直,∠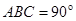 ,
,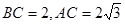 ,且
,且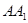 ⊥
⊥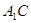 ,
,
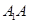 与平面
与平面 是否垂直,并说明理由;
是否垂直,并说明理由; 与底面
与底面
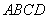 的边长为
的边长为 ,点
,点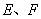 分别在
分别在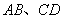 上,并且满足
上,并且满足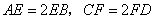 ,如图乙,将直角梯形
,如图乙,将直角梯形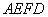 沿
沿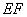 折到
折到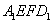 的位置,使点
的位置,使点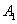 在
在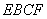 上的射影
上的射影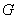 恰好在
恰好在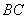 上.
上.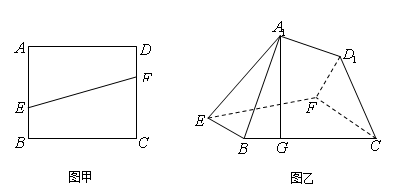
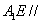 平面
平面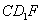 ;
;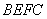 与平面
与平面 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则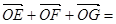 ( )
( )



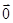
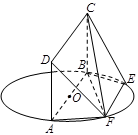
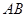 为圆
为圆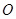 的直径,点
的直径,点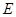 、
、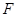 在圆
在圆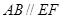 ,矩形
,矩形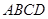 所在的平面与圆
所在的平面与圆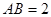 ,
,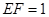 .
.
 平面
平面 ;
;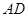 的长为何值时,平面
的长为何值时,平面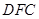 与平面
与平面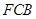 所成的锐二面角的大小为
所成的锐二面角的大小为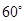 ?
?
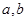 为两条直线,
为两条直线,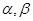 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( ) 且
且 ,则
,则
 ,则
,则
 ,
, 则
则 则
则