题目内容
【题目】下列命题:
①动点M到二定点A、B的距离之比为常数![]() 则动点M的轨迹是圆
则动点M的轨迹是圆
②椭圆![]() 的离心率为
的离心率为![]() ,则
,则![]()
③双曲线![]() 的焦点到渐近线的距离是
的焦点到渐近线的距离是![]()
④已知抛物线![]() 上两点
上两点![]() (
(![]() 是坐标原点),则
是坐标原点),则![]()
以上命题正确的是( )
A.②③④B.①④
C.①③D.①②③
【答案】D
【解析】
对于①,通过建立坐标系,求出动点的轨迹方程判断出正确;利用椭圆中三个参数的关系判断出②对;对于③,据双曲线的方程求出焦点坐标和渐近线方程,利用点到直线的距离公式判断出正确;对于④,利用向量垂直的充要条件判断出其错
对于①,以AB所在的直线为x轴,AB的中垂线为y轴建立坐标系,设M(x,y),A(-a,0),B(a,0),则有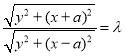 化简得(1-λ2)x2+(1-λ2)y2+(2a+2aλ2)x+a2-a2λ2=0,所以动点M的轨迹是圆,①正确;
化简得(1-λ2)x2+(1-λ2)y2+(2a+2aλ2)x+a2-a2λ2=0,所以动点M的轨迹是圆,①正确;
对于②,![]() ,所以
,所以![]() ,所以a2=2c2,所以椭圆中有b2=a2-c2=c2,所以b=c,所以②正确;
,所以a2=2c2,所以椭圆中有b2=a2-c2=c2,所以b=c,所以②正确;
对于③,双曲线![]() 的焦点坐标为(±c,0),渐近线的方程为:
的焦点坐标为(±c,0),渐近线的方程为:![]() ,根据点到直线的距离公式得到距离=
,根据点到直线的距离公式得到距离=![]() .所以③正确;
.所以③正确;
对于④,因为OA⊥OB,所以x1x2+y1y2=0,又因为y2=2px,所以y12=2px1,y22=2px2,所以y1y2=-4p2.④不正确
故选:D.

【题目】某校在学年期末举行“我最喜欢的文化课”评选活动,投票规则是一人一票,高一(1)班44名学生和高一(7)班45名学生的投票结果如下表(无废票):
语文 | 数学 | 外语 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
高一(1)班 | 6 | 9 | 7 | 5 | 4 | 5 | 3 | 3 | 2 |
高一(7)班 |
| 6 |
| 4 | 5 | 6 | 5 | 2 | 3 |
该校把上表的数据作为样本,把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求![]() 的所有取值;
的所有取值;
(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取![]() 位同学,设随机变量
位同学,设随机变量![]() 为投票给地理学科的人数,求
为投票给地理学科的人数,求![]() 的分布列和期望;
的分布列和期望;
(Ⅲ)当![]() 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
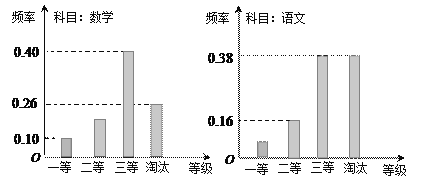
【题目】某企业对现有设备进行了改造,为了了解设备改造后的效果,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测其质量指标值,若质量指标值在![]() 内,则该产品视为合格品,否则视为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内,则该产品视为合格品,否则视为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

(1)完成![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关:
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关:
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价180元;质量指标值落在
内的定为一等品,每件售价180元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价150元;其他的合格品定为三等品,每件售价120元.根据频数分布表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价150元;其他的合格品定为三等品,每件售价120元.根据频数分布表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()