题目内容
【题目】设函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)当a=0时,求函数f (x)的单调减区间;
(2)已知函数f (x)的导函数f (x)有三个零点x1,x2,x3(x1 x2 x3).①求a的取值范围;②若m1,m2(m1 m2)是函数f (x)的两个零点,证明:x1m1x1 1.
【答案】(1)![]() ;(2)①
;(2)①![]() ②证明见解析
②证明见解析
【解析】
(1)当![]() 时,
时,![]() ,令
,令![]() ,即可求得单调减区间;
,即可求得单调减区间;
(2)①![]() ,令
,令![]() ,将
,将![]() 有三个零点转化为
有三个零点转化为![]() 有三个零点,对
有三个零点,对![]() 求导,可得
求导,可得![]() 的单调性,进而得到
的单调性,进而得到![]() 的范围;
的范围;
②将![]() 有两个零点转化为方程
有两个零点转化为方程![]() 有两个零点,则可得
有两个零点,则可得![]() ,
,![]() ,进而得到
,进而得到![]() ,
,![]() ,从而得证
,从而得证
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,可得
,可得![]() ,
,
![]() 的单调减区间为
的单调减区间为![]()
(2)①由题,
![]() ,
,
![]() ,
,![]() ,设
,设![]() ,
,
![]() 是
是![]() 的三个零点,
的三个零点,
![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 单调递减,不符合条件;
单调递减,不符合条件;
当![]() 时,令
时,令![]() ,则
,则![]() ,
,
![]() 在
在 ,
, 单调递增,在
单调递增,在 ,
,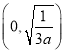 单调递减,
单调递减,
![]() ,
,
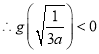 ,即
,即 ,
,
![]()
![]() ,
,
![]()
②![]() 是
是![]() 的两个零点,令
的两个零点,令![]() ,则方程
,则方程![]() 的两根分别为
的两根分别为![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
由①![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,即
,即![]() ,
,
故![]()

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目