题目内容
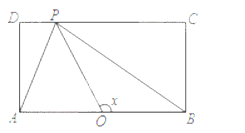
【题目】如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3. 
(1)证明:平面ACF⊥平面BEFD
(2)若二面角A﹣EF﹣C是二面角,求直线AE与平面ABCD所成角的正切值.
【答案】
(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,
∵BE⊥平面ABCD,∴BE⊥AC,
∴AC⊥平面BEFD,
∵AC平面ACF,∴平面ACF⊥平面BEFD
(2)解:设AC与BD的交点为O,由(1)得AC⊥BD,
分别以OA,OB为x轴,y轴,建立空间直角坐标系,
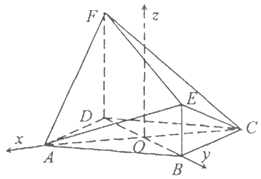
∵BE⊥平面ABCD,∴BE⊥BD,
∵DF∥BE,∴DF⊥BD,
∴BD2=EF2﹣(DF﹣BE)2=8,∴BD=2 ![]() .
.
设OA=a,(a>0),
由题设得A(a,0,0),C(﹣a,0,0),E(0, ![]() ),F(0,﹣
),F(0,﹣ ![]() ,2),
,2),
设m=(x,y,z)是平面AEF的法向量,
则 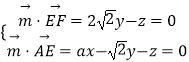 ,取z=2
,取z=2 ![]() ,得
,得 ![]() =(
=( ![]() ),
),
设 ![]() 是平面CEF的一个法向量,
是平面CEF的一个法向量,
则 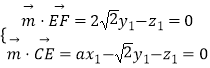 ,取
,取 ![]() ,得
,得 ![]() =(﹣
=(﹣ ![]() ,1,2
,1,2 ![]() ),
),
∵二面角A﹣EF﹣C是直二面角,
∴ ![]() =﹣
=﹣ ![]() +9=0,解得a=
+9=0,解得a= ![]() ,
,
∵BE⊥平面ABCD,
∴∠BAE是直线AE与平面ABCD所成的角,
∴AB= ![]() =2,∴tan
=2,∴tan ![]() .
.
∴直线AE与平面ABCD所成角的正切值为 ![]() .
.
【解析】(1)推导出AC⊥BD,BE⊥AC,从而AC⊥平面BEFD,由此能证明平面ACF⊥平面BEFD.(2)设AC与BD的交点为O,分别以OA,OB为x轴,y轴,建立空间直角坐标系,利用向量法能求出直线AE与平面ABCD所成角的正切值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】![]() 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度平分如下:
某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度平分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)(I)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可)
(2)(II)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
|
|
|
|
|
|
|
|
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立。根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。