题目内容
等差数列{an}的前n项和为Sn,公差d<0,若存在正整数m(m≥3),使得am=Sm,则当n>m(n∈N*)时
- A.Sn>an
- B.Sn≥an
- C.Sn<an
- D.Sn≤an
C
分析:本题考查的知识点是等差数列的前n项和,及等差数列的性质,由等差数列{an}的前n项和为Sn,公差d<0,及存在正整数m(m≥3),使得am=Sm,我们可以构造一个方程组,判断出基本项(首项与公差)的关系,然后代入n>m,利用作差法即可判断出Sn与an的关系.
解答:∵am=Sm,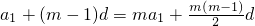 ,
,
∴(2m-2)a1=(m-1)(2-m)d
∴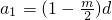 ,
,
∴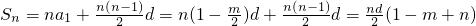 ,
,
又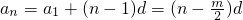 ,
,
∴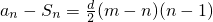
又∵m≥3,m<n,d<0,
∴ ,
,
故an>Sn.
点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.
分析:本题考查的知识点是等差数列的前n项和,及等差数列的性质,由等差数列{an}的前n项和为Sn,公差d<0,及存在正整数m(m≥3),使得am=Sm,我们可以构造一个方程组,判断出基本项(首项与公差)的关系,然后代入n>m,利用作差法即可判断出Sn与an的关系.
解答:∵am=Sm,
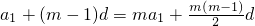 ,
,∴(2m-2)a1=(m-1)(2-m)d
∴
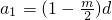 ,
,∴
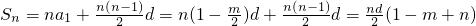 ,
,又
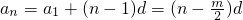 ,
,∴
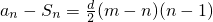
又∵m≥3,m<n,d<0,
∴
 ,
,故an>Sn.
点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |