题目内容
7．下列结论正确的是（ ）| A． | 若a＞b，则ac＞bc | B． | 若a＞b，则a2＞b2 | ||
| C． | 若a+c＜b+c，c＜0，则a＞b | D． | 若$\sqrt{a}$＞$\sqrt{b}$，则a＞b |
分析 通过举反例可得A、B、C不成立，里用不等式的性质可得D成立，从而得出结论．
解答 解：当c=0时，A不成立；当a=-1、b=-2时，B不成立；
令c=-1，则由a+c＜b+c，可得a＜b，故C不成立；
若$\sqrt{a}$＞$\sqrt{b}$，则一定能推出a＞b，故D成立，
故选：D．
点评 本题主要考查不等式的基本性质，通过举反例来说明某个结论不成立，是一种简单有效的方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．已知数列{an}的通项公式为an=2n+3，则（ ）
| A． | {an}是公比为2的等比数列 | B． | {an}是公比为3的等比数列 | ||
| C． | {an}是公差为2的等差数列 | D． | {an}是公差为3的等差数列 |
12．某产品的广告费用x（万元）与销售额y（万元）的统计数据如表，根据右表可得回归方程$\hat y=\hat bx+\hat a$中的$\hat a=0$，据此模型预报广告费用为6万元时销售额为（ ）
| x | 4 | 2 | 3 | 5 |
| y | 38 | 20 | 31 | 51 |
| A． | 50 | B． | 60 | C． | 63 | D． | 59 |
19．某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取100个，整理得到数据分组及频率分布表和频率分布直方图：
（Ⅰ）写出频率分布直方图中的a的值，并作出甲种酸奶日销售量的频率分布直方图；
答：a=0.015；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s12，s22，试比较s12与s22的大小．（只需写出结论）．
答：s12＜s22．
| 分组 （日销售量） | 频率 （甲种酸奶） |
| [0，10] | 0.10 |
| （10，20] | 0.20 |
| （20，30] | 0.30 |
| （30，40] | 0.25 |
| （40，50] | 0.15 |
答：a=0.015；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s12，s22，试比较s12与s22的大小．（只需写出结论）．
答：s12＜s22．
16．若圆C的半径为1，其圆心C与点（1，0）关于直线x+y=0对称，则圆C的标准方程为（ ）
| A． | x2+（y-1）2=1 | B． | x2+（y+1）2=1 | C． | （x-1）2+y2=1 | D． | （x+1）2+y2=1 |
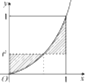如图，由曲线y=x2和直线y=t2（0＜t＜1），x=1，x=0所围成的图形（阴影部分）的面积的最小值是$\frac{1}{4}$．