题目内容
【题目】如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1 , CC1的中点,且BE⊥B1F. 
(1)求证:B1F⊥EC1;
(2)求二面角C1﹣BE﹣C的余弦值.
【答案】
(1)证明:分别取BC1,BC中点D,G,连结ED,AG,
∵ABC﹣A1B1C1是直三棱柱,且底面是正三角形,
∴AG⊥面BCC1B1,
又∵E,D都是中点,∴ED∥AG,则ED⊥面BCC1B1,可得ED⊥B1F,
已知BE⊥B1F,且BE∩ED=E,∴B1F⊥面BEC1,则B1F⊥EC1
(2)解:由(Ⅰ)知B1F⊥面BEC1,∴B1F⊥BC1,则△B1C1F∽△BB1C1,
∴ ![]() ,设BB1=a,则C1F=
,设BB1=a,则C1F= ![]() ,代入得a=
,代入得a= ![]() ,
,
以O为原点,OE为x轴,OC为y轴,过O作平面ABC的垂线为z轴,建立如图坐标系O﹣xyz,
得C(0,2,0),B( ![]() ,0,0),E(0,﹣2,
,0,0),E(0,﹣2, ![]() ),
),
C1(0,2,4 ![]() ),B1(
),B1( ![]() ,0,
,0, ![]() ),F(0,2,2
),F(0,2,2 ![]() ).
).
∵B1F⊥面BEC1,∴平面BEC1的一个法向量为 ![]() ;
;
设平面BEC的一个法向量为 ![]() ,
,
则 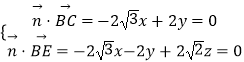 ,取x=
,取x= ![]() ,得y=3,z=
,得y=3,z= ![]() .
.
∴ ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
∴二面角C1﹣BE﹣C的余弦值为 ![]() .
.
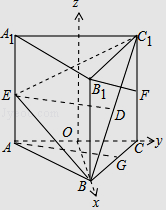
【解析】(1)分别取BC1 , BC中点D,G,连结ED,AG,推导出AG⊥面BCC1B1 , 从而ED⊥B1F,BE⊥B1F,由此能证明B1F⊥面BEC1 , 进一步得到B1F⊥EC1;(2)以O为原点,OE为x轴,OC为y轴,过O作平面ABC的垂线为z轴,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角C1﹣BE﹣C的余弦值.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据:出生时间在晚上的男婴为24人,女婴为8人;出生时间在白天的男婴为31人,女婴为26人.
(1)将2×2列联表补充完整.
性别 | 出生时间 | 总计 | |
晚上 | 白天 | ||
男婴 | |||
女婴 | |||
总计 | |||
(2)能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系?
【题目】2016年备受瞩目的二十国集团领导人第十一次峰会于9月4~5日在杭州举办,杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人,为测试培训效果,采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人,对其做G20峰会主题及相关服务职责进行测试,将其所得分数(分数都在60~100之间)制成频率分布直方图如下图所示,若得分在90分及其以上(含90分)者,则称其为“G20通”. 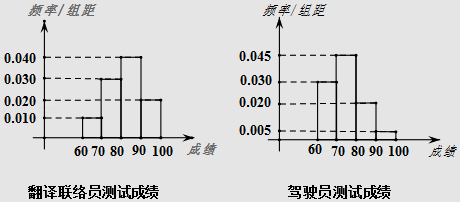
(Ⅰ)能否有90%的把握认为“G20通”与所从事工作(翻译联络员或驾驶员)有关?
(Ⅱ)从参加测试的成绩在80分以上(含80分)的驾驶员中随机抽取4人,4人中“G20通”的人数为随机变量X,求X的分布列与数学期望.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附参考公式与数据: ![]() .
.


