题目内容
已知直线ax+by+c=0与圆O:x2+y2=1相交于A,B两点,且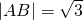 ,以A,B为切点的两条切线的夹角为________.
,以A,B为切点的两条切线的夹角为________.

分析:取AB的中点C,连接OC,|利用圆的切线性质求出∠AOB的大小,设两切线的交点为N,再根据四边形OANB为圆内接四边形,可得∠AOB 与∠ANB互补,由此求得∠ANB的值.
解答:
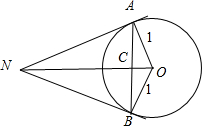 解:取AB的中点C,连接OC,|AB|=
解:取AB的中点C,连接OC,|AB|= ,则|AC|=
,则|AC|= ,|OA|=1,故sin∠AOC=
,|OA|=1,故sin∠AOC=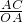 =
= ,
,∴∠AOC=
 ,
,∴∠AOB=
 .
.设两切线的交点为N,再由圆的切线性质可得,四边形OANB为圆内接四边形,故∠AOB 与∠ANB互补,
∴∠ANB=π-
 =
= ,
,故答案为
 .
.点评:本题主要考查了直线和圆的方程的应用,以及向量的数量积公式的应用,同时考查了计算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知直线Ax+By+C=0(其中A2+B2=C2,C≠0)与圆x2+y2=4交于M,N,O是坐标原点,则
•
=( )
| OM |
| ON |
| A、-1 | B、-1 | C、-2 | D、2 |