题目内容
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
当高为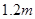 时,容器的容积最大,最大容积为
时,容器的容积最大,最大容积为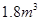 .
.
解析试题分析:先设容器底面短边长为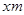 ,利用长方体的体积公式求得其容积表达式,再利用导数研究它的单调性,进而得出此函数的最大值即可.
,利用长方体的体积公式求得其容积表达式,再利用导数研究它的单调性,进而得出此函数的最大值即可.
试题解析:设容器底面短边的边长为 ,容积为
,容积为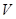 ,则底面另一边长为
,则底面另一边长为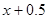 ,高为:
,高为: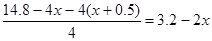 .
.
由题意知: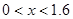 ,
,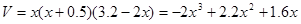 ,
,
则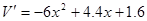 .
.
令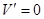 ,解之得:
,解之得: (舍去).
(舍去).
又当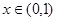 时,
时,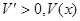 为增函数;当
为增函数;当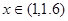 时,
时,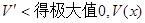 为减函数.
为减函数.
所以 在
在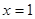 时取得极大值
时取得极大值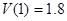 ,这个极大值就是
,这个极大值就是 在
在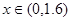 时的最大值,即
时的最大值,即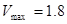 ,此时容器的高为1.2.
,此时容器的高为1.2.
所以当高为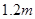 时,容器的容积最大,最大值为
时,容器的容积最大,最大值为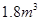 .
.
考点:函数模型的选择与应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
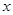 元,则本年度新增用电量
元,则本年度新增用电量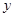 (亿千瓦时)与
(亿千瓦时)与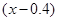 元成反比例.又当
元成反比例.又当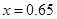 时,
时,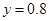 .
.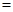 用电量
用电量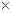 (实际电价-成本价)]
(实际电价-成本价)]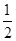 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用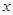 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数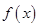 .
.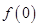 的值,并解释其实际意义;
的值,并解释其实际意义;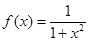 ,现有
,现有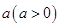 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由. (x∈R,且x≠2).
(x∈R,且x≠2). 的单调区间;
的单调区间;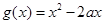 与函数
与函数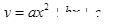 的图象与
的图象与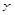 轴交于
轴交于 的充要条件为
的充要条件为 .
. ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立. 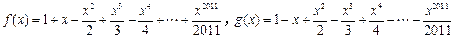 ,设
,设 内,则
内,则 的最小值为_________
的最小值为_________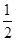 )时恒成立,求实数a的取值范围.
)时恒成立,求实数a的取值范围.