题目内容
求证:二次函数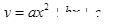 的图象与
的图象与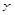 轴交于
轴交于 的充要条件为
的充要条件为 .
.
必要性和充分性.
解析试题分析:证明充要条件必须分别证明必要性和充分性;对于必要性,显然由题意可知 是方程
是方程 的一个根,代入方程可得:
的一个根,代入方程可得: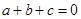 ;对于充分性,把
;对于充分性,把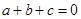 ,代入二次函数化简即得
,代入二次函数化简即得 时
时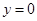 .
.
证明:(1)必要性:由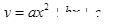 的图象与
的图象与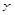 轴交于
轴交于 ,可知方程
,可知方程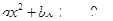 有一个根为1,即
有一个根为1,即 ;
;
(2)充分性:若 ,则
,则 ,
,
当 时,
时, ,即函数
,即函数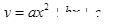 的图象过
的图象过 点.
点.
故函数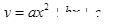 的图象与
的图象与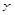 轴交于
轴交于 点的充要条件为
点的充要条件为 .
.
考点:充要条件

练习册系列答案
相关题目
 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 ,圆心角为
,圆心角为 (弧度).
(弧度).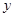 ,求
,求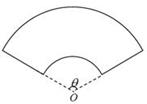
 .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围;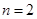 ,若对任意
,若对任意 恒成立,求
恒成立,求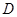 (分贝)由公式
(分贝)由公式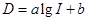 (
(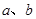 为非零常数)给出,其中
为非零常数)给出,其中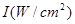 为声音能量.
为声音能量.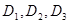 满足
满足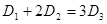 时,求对应的声音能量
时,求对应的声音能量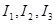 满足的等量关系式;
满足的等量关系式;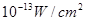 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为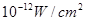 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪. ,求Tn.
,求Tn.