题目内容
某渔业公司年初用49万元购买一艘捕鱼船,第一年各种费用6万元,以后每年都增加2万元,每年捕鱼收益25万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以18万元出售该渔船;②总纯收入获利最大时,以9万元出售该渔船.问哪种方案最合算?
(1)渔业公司第3年开始获利.(2)方案①较合算.
解析试题分析:(1)由题意列出获利y与年份n的函数关系,然后求解不等式得到n的范围,根据n是正的自然数求得n的值;
(2)用获利除以年份得到年平均获利,利用不等式求出最大值,求出获得的总利润,利用配方法求出获得利润的最大值,求出总获利,比较后即可得到答案.
试题解析:(1)第n年开始获利,设获利为y万元,则
y=25n-[6n+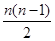 ×2]-49=-n2+20n-49 2分
×2]-49=-n2+20n-49 2分
由y=-n2+20n-49>0得10-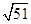 <n<10+
<n<10+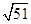 4分
4分
又∵n∈N*,∴n=3,4
∴n=3时,即该渔业公司第3年开始获利. 5分
(2)方案①:年平均获利为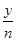 =-n-
=-n- +20≤-2
+20≤-2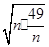 +20=6(万元) 7分
+20=6(万元) 7分
当n=7时,年平均获利最大,若此时卖出,共获利6×7+18=60(万元) 8分
方案②:y=-n2+20n-49=-(n-10)2+51
当且仅当n=10时,即该渔业公司第10年总额最大,若此时卖出,共获利51+9=60万元 11分
因为两种方案获利相等,但方案②所需的时间长,所以方案①较合算. 12分
考点:函数模型的选择及应用;简单的建模思想;利用基本不等式求最值;配方法.

练习册系列答案
相关题目
 x,求使每月售货总金额有所增加的x值的范围.
x,求使每月售货总金额有所增加的x值的范围. ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个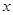 都成立,则称函数
都成立,则称函数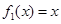 是否为 “(
是否为 “(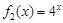 是“(
是“(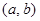 ;
; 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对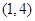 ,当
,当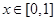 时,
时,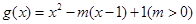 ,若当
,若当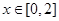 时,都有
时,都有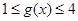 ,试求
,试求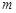 的取值范围.
的取值范围.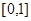 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: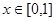 ,总有
,总有 ;
;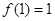 ;
; 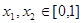 ,且
,且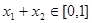 时,
时,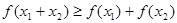 成立.
成立.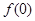 的值;
的值;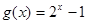 在区间
在区间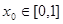 ,使得
,使得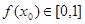 ,且
,且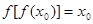 ,求证:
,求证: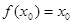 .
. .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围;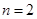 ,若对任意
,若对任意 恒成立,求
恒成立,求
 的最小值记为
的最小值记为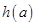 ,求
,求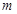 ,
,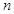 同时满足以下条件:①
同时满足以下条件:① ;②当
;②当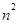 ,
, ];若存在,求出
];若存在,求出