题目内容
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为双曲线
,离心率为双曲线![]() 离心率的一半,直线
离心率的一半,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .直线
.直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两个相异点,且
两个相异点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在实数![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)设出椭圆的标准方程,利用离心率、四边形的周长进行求解;(Ⅱ)利用平面向量的线性运算得到![]() 的关系,联立直线与椭圆的方程,得到关于
的关系,联立直线与椭圆的方程,得到关于![]() 的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
试题解析:(Ⅰ)根据已知设椭圆![]() 的方程为
的方程为![]() ,焦距为
,焦距为![]() ,
,
由已知得![]() ,∴
,∴![]() .
.
∵以椭圆![]() 的长轴和短轴为对角线的四边形的周长为
的长轴和短轴为对角线的四边形的周长为![]() ,
,
∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)根据已知得![]() ,由
,由![]() ,得
,得![]() .
.
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
若![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,即
,即![]() .
.
∴![]() 能使
能使![]() 成立.
成立.
若![]() ,则
,则![]() ,解得
,解得![]() .
.
设![]() ,由
,由![]() 得
得![]() ,
,
由已知得![]() ,即
,即![]() .
.
且![]() .…10分
.…10分
由![]() 得
得![]() ,即
,即![]() .∴
.∴![]() ,
,
∴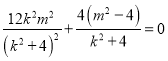 ,即
,即![]() .
.
当![]() 时,
时, ![]() 不成立.∴
不成立.∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() ,解得
,解得![]() 或
或![]() .
.
综上述,当![]() 或
或![]() 或
或![]() 时,
时, ![]() .
.

【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的最小二乘法估计公式分别为:![]() =
=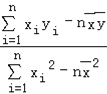 ,
,![]() =
=![]() ﹣
﹣![]()
![]() ,
,
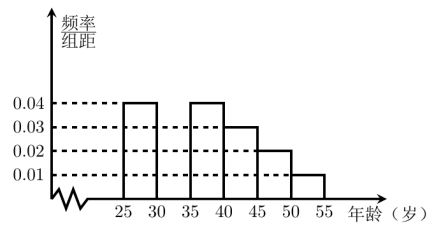
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.