Question

15．如图，圆O的直径为AB，半径OC垂直于AB，M为AO上一点，CM的延长线交圆O于N，过N点的切线交BA的延长线于P．
（Ⅰ）求证：PM²=PA•PB；
（Ⅱ）若圆O的半径为4$\sqrt{3}$，OA=$\sqrt{3}$OM，求PN的长．

Answer 1

分析 （ I）利用切线的性质、圆的性质、切割线定理即可得出；
（Ⅱ）求出OM=4，∠OPN=60°，利用tan∠OPN=$\frac{ON}{PN}$=$\sqrt{3}$，求PN的长．

解答 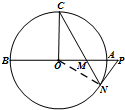（ I）证明：如图，连接ON，则ON⊥PN，且△OCN为等腰三角形，
则∠OCN=∠ONC．
因为∠PMN=∠OMC=90°-∠OCN，∠PNM=90°-∠ONC，
所以∠PMN=∠PNM，所以PM=PN．…（3分）
根据切割线定理，有PN²=PA•PB，所以PM²=PA•PB．…（5分）
（ II）解：因为OA=$\sqrt{3}$OM=4$\sqrt{3}$，所以OM=4．
在Rt△COM中，tan∠CMO=$\frac{OC}{OM}$=$\sqrt{3}$，所以∠CMO=60°．…（6分）
所以∠CMO=∠PMN=∠PNM=60°，所以△PMN是等边三角形，
所以∠OPN=60°．…（8分）
在Rt△OPN中，tan∠OPN=$\frac{ON}{PN}$=$\sqrt{3}$，所以PN=4．…（10分）

点评 熟练掌握切线的性质、圆的性质、切割线定理是解题的关键．