题目内容
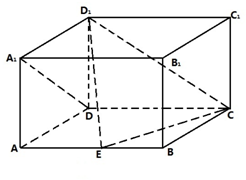 如图,在长方体ABCD-A1B1C1D1中 AD=AA1=1,AB=2
如图,在长方体ABCD-A1B1C1D1中 AD=AA1=1,AB=2 (1)证明:当点E在棱AB移动时,D1E⊥A1D;
(2)(理)在棱AB上是否存在点E,是二平面角D1-EC-D的平面角为
| π | 6 |
(文)在棱AB上否存在点E使CE⊥面D1DE若存在,求出AE的长;若不存在,请说明理由.
分析:(1)连接AD1,由EA⊥平面ADD1A1,A1D?平面ADD1A1,证出A1D⊥EA,再在正方形ADD1A1得出A1D⊥AD1,证出A1D⊥平面AD1E后可证D1E⊥A1D.
(2)(理)存在.连接DE,过D作DH⊥EC,交EC于H,连接D1H,则∠D1HD为二面角D1-EC-D的平面角,即∠D1HD=
,设AE=x(0≤x≤2),在RT△D1DH中利用tan
=
,列出方程
=
,考察方程的解得情况作出回答.
(文)存在点E.设AE=x(0≤x≤2),则BE=2-x,在RT△DEC中由勾股定理列出关于x的方程,考察方程的解得情况作出回答.
(2)(理)存在.连接DE,过D作DH⊥EC,交EC于H,连接D1H,则∠D1HD为二面角D1-EC-D的平面角,即∠D1HD=
| π |
| 6 |
| π |
| 6 |
| D1D |
| DH |
| 2 | ||
|
| ||
| 3 |
(文)存在点E.设AE=x(0≤x≤2),则BE=2-x,在RT△DEC中由勾股定理列出关于x的方程,考察方程的解得情况作出回答.
解答:(1)证明:连接AD1,由长方体的结构特征,EA⊥平面ADD1A1,A1D?平面ADD1A1,∴A1D⊥EA,
由AD=AA1=1,则四边形ADD1A1是正方形,∴A1D⊥AD1,
又∵EA∩AD1=A,∴A1D⊥平面AD1E,
∵D1E?平面AD1E,
∴D1E⊥A1D.
(2)解:存在点E,使二平面角D1-EC-D的平面角为
,此时AE=2-
.
连接DE,过D作DH⊥EC,交EC于H,连接D1H,
在长方体ABCD-A1B1C1D1中,DD1⊥平面ABCD,EC?平面ABCD,
∴DD1⊥EC,又∵DH∩DD1=D,
∴EC⊥平面D1DH,∵D1H?平面D1DH,∴EC⊥D1H,
∴∠D1HD为二面角D1-EC-D的平面角,即∠D1HD=
设AE=x(0≤x≤2),则EB=2-x,进而EC=
,
在△DEC中,利用面积相等的关系有:EC×DH=CD×AD,
DH=
,在RT△D1DH中,
∵∠D1HD=
,
∴tan
=
,即
=
解得x=2-
(0≤x≤2),所以存在点E,使二平面角D1-EC-D的平面角为
,此时AE=2-
.
(文)存在点E.此时E为AB中点.CE⊥面D1DE,
∴CE⊥DE,设AE=x(0≤x≤2),则BE=2-x,
由勾股定理得DE2=AD2+AE2=1+x2,CE2=CB2+BE2=1+(2-x)2,在RT△DEC中,CD2=DE2+CE2=,4=1+x2+1+(2-x)2,
整理化简得出x2-2x+1=0,x=1,此时E为AB中点.
由AD=AA1=1,则四边形ADD1A1是正方形,∴A1D⊥AD1,
又∵EA∩AD1=A,∴A1D⊥平面AD1E,
∵D1E?平面AD1E,
∴D1E⊥A1D.
(2)解:存在点E,使二平面角D1-EC-D的平面角为
| π |
| 6 |
| ||
| 3 |
连接DE,过D作DH⊥EC,交EC于H,连接D1H,
在长方体ABCD-A1B1C1D1中,DD1⊥平面ABCD,EC?平面ABCD,
∴DD1⊥EC,又∵DH∩DD1=D,
∴EC⊥平面D1DH,∵D1H?平面D1DH,∴EC⊥D1H,
∴∠D1HD为二面角D1-EC-D的平面角,即∠D1HD=
| π |
| 6 |
设AE=x(0≤x≤2),则EB=2-x,进而EC=
| 1+(2-x)2 |
在△DEC中,利用面积相等的关系有:EC×DH=CD×AD,
DH=
| 2 | ||
|
∵∠D1HD=
| π |
| 6 |
∴tan
| π |
| 6 |
| D1D |
| DH |
| 2 | ||
|
| ||
| 3 |
解得x=2-
| ||
| 3 |
| π |
| 6 |
| ||
| 3 |
(文)存在点E.此时E为AB中点.CE⊥面D1DE,
∴CE⊥DE,设AE=x(0≤x≤2),则BE=2-x,
由勾股定理得DE2=AD2+AE2=1+x2,CE2=CB2+BE2=1+(2-x)2,在RT△DEC中,CD2=DE2+CE2=,4=1+x2+1+(2-x)2,
整理化简得出x2-2x+1=0,x=1,此时E为AB中点.
点评:本题考察直线和直线、直线和平面垂直关系,二面角的大小度量及应用,考查方程思想,空间想象能力、推理论证、计算、转化能力.

练习册系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.