题目内容
（2013•未央区三模）若向量
=（cosθ，sinθ），
=(
，-1)，则
的最大值为
| a |
| b |
| 3 |
|
3
3
．分析：先求得
-
=（cosθ-
，sinθ+1），|
|=1，|
|=2，
•
=
cosθ-sinθ．化简 (
-
)2=5-4sin（θ+
），可得(
-
)2的最大值为9，从而得到
的最大值．
| a |
| b |
| 3 |
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| π |
| 3 |
| a |
| b |
|
解答：解：向量
=（cosθ，sinθ），
=(
，-1)，
则
-
=（cosθ-
，sinθ+1），|
|=1，|
|=2，
•
=
cosθ-sinθ．
∴(
-
)2=
2-2
•
+
2=1-2
cosθ+2sinθ+4=5-2（
cosθ-sinθ）=5-4sin（θ+
），
故(
-
)2的最大值为9，故
最大值为3，
故答案为3．
| a |
| b |
| 3 |
则
| a |
| b |
| 3 |
| a |
| b |
| a |
| b |
| 3 |
∴(
| a |
| b |
| a |
| a |
| b |
| b |
| 3 |
| 3 |
| π |
| 3 |
故(
| a |
| b |
|
故答案为3．
点评：本题主要考查两个向量的数量积的定义，两个向量的数量积公式的应用，求向量的模，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
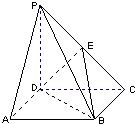（2013•未央区三模）如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．
（2013•未央区三模）某三棱锥的三视图如图所示，该三棱锥的体积是为（ ）