题目内容
【题目】从某企业生产的产品的生产线上随机抽取 件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图：
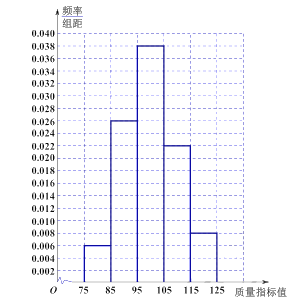
(Ⅰ) 估计这批产品质量指标值的样本平均数
和样本方差
(同一组中的数据用该组区间的中点值作代表)；
(Ⅱ) 若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中
为产品质量指标值):
当
, 该产品定为一等品,企业可获利 200 元；
当
且
，该产品定为二等品,企业可获利 100 元；
当
且
，该产品定为三等品,企业将损失 500 元；
否则该产品定为不合格品,企业将损失 1000 元．
(ⅰ)若测得一箱产品(5 件)的质量指标数据分别为：76、85、93、105、112,求该箱产品的利润；
(ⅱ)设事件
；事件
；事件
. 根据经验,对于该生产线上的产品,事件
发生的概率分别为0.6826、0.9544、0.9974.根据以上信息,若产品预计年产量为10000件,试估计该产品年获利情况.(参考数据:
)
【答案】（1）平均数的估计值为 100,方差的估计值为 104．（2）100元，
元
【解析】试题分析：（1）根据组中值与对应区间概率乘积的和计算平均数，根据方差公式求方差，（2）(ⅰ)先根据定义分别求出各箱对应利润，再求和，(ⅱ) )根据提供的概率分布,估计出10000件产品中三个等级的件数，再根据定义分别求出各箱对应利润，最后求和.
试题解析：(Ⅰ) 质量指标的样本平均数
,
质量指标的样本的方差
,这种产品质量指标的平均数的估计值为 100,方差的估计值为 104．
(Ⅱ)因
.
(i)计算得5件产品中有一等品两件：93,105；二等品两件：85,112；三等品一件：76.
故根据规则,获利为: 
元．
(ⅱ)根据提供的概率分布,该企业生产的 10000件产品中一等品大约为
件,
二等品大约为
件,三等品
件,
不合格品大约为
件.
估计年获利为: 
元.
