题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点.
上的两个不同点.
(1)若![]() ,且点
,且点![]() 所在直线方程为
所在直线方程为![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 的斜率之积为
的斜率之积为![]() ,线段
,线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接
,连接![]() 并廷长交椭圆
并廷长交椭圆![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设![]() ,由
,由![]() 得
得![]() ,化简得
,化简得![]() ,联立直线方程与椭圆方程,利用韦达定理代入化简得
,联立直线方程与椭圆方程,利用韦达定理代入化简得![]() 的值;(2)根据条件得
的值;(2)根据条件得![]() ,设
,设![]() ,则得点
,则得点![]() ,代入椭圆方程,利用
,代入椭圆方程,利用![]() ,
, ![]() ,以及由直线
,以及由直线![]() 斜率之积为
斜率之积为![]() ,得
,得![]() ,代入化简可得
,代入化简可得![]() 的值.
的值.
试题解析:(1)由题知![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
设![]() ,将直线
,将直线![]() 代入椭圆方程得:
代入椭圆方程得:![]() ,
,
∴由韦达定理知:![]() .
.
∵![]() ,∴
,∴![]() ,即
,即
![]() ,
,
将![]() 代入得
代入得![]() ,即
,即![]() ,
,
解得![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
(2)设![]() ,
,![]() ,
,
由题知![]() ,∴
,∴![]() ,
,
∴![]() .
.
又∵![]() ,∴
,∴![]() ,即
,即
![]() .
.
∵点![]() 在椭圆
在椭圆![]() 上,∴
上,∴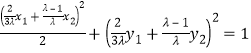 ,
,
即![]() .
.![]()
∵![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,①
,① ![]() ,②
,②
又直线![]() 斜率之积为
斜率之积为![]() ,∴
,∴![]() ,即
,即![]() ,③
,③
将①②③代入![]() 得
得![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目
【题目】某协会对![]() ,
,![]() 两家服务机构进行满意度调查,在
两家服务机构进行满意度调查,在![]() ,
,![]() 两家服务机构提供过服务的市民中随机抽取了
两家服务机构提供过服务的市民中随机抽取了![]() 人,每人分别对这两家服务机构进行独立评分,满分均为
人,每人分别对这两家服务机构进行独立评分,满分均为![]() 分.整理评分数据,将分数以
分.整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到
,得到![]() 服务机构分数的频数分布表,
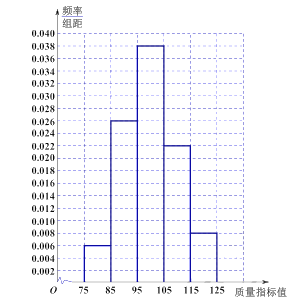
服务机构分数的频数分布表,![]() 服务机构分数的频率分布直方图:
服务机构分数的频率分布直方图:


定义市民对服务机构评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 | 0 | 1 | 2 |
(1)在抽样的![]() 人中,求对
人中,求对![]() 服务机构评价“满意度指数”为
服务机构评价“满意度指数”为![]() 的人数;
的人数;
(2)从在![]() ,
,![]() 两家服务机构都提供过服务的市民中随机抽取
两家服务机构都提供过服务的市民中随机抽取![]() 人进行调查,试估计对
人进行调查,试估计对![]() 服务机构评价的“满意度指数”比对
服务机构评价的“满意度指数”比对![]() 服务机构评价的“满意度指数”高的概率;
服务机构评价的“满意度指数”高的概率;
(3)如果从![]() ,
,![]() 服务机构中选择一家服务机构,以满意度出发,你会选择哪一家?说明理由.
服务机构中选择一家服务机构,以满意度出发,你会选择哪一家?说明理由.