Question

【题目】已知函数f（x）=x|x-a|+bx．

（1）若a=2，且f（x）是R上的增函数，求实数b的取值范围；

（2）当b=0时，若关于x的方程f（x）=x+1有三个实根，求a的取值范围．

Answer 1

【答案】（1）b≥2（2）a＞3或者a＜-1

【解析】

（1）写出解析式，利用单调性求解；

（2）将关于x的方程f（x）=x+1的实根个数问题转化为的图像的交点个数问题，再由图象得出结论．

解：（1）当a=2，f（x）=x|x-2|+bx=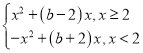，f（x）是R上的增函数，

则，，故b≥2．

（2）b=0，f（x）=x|x-a|=x+1，若x=0显然不成立，

上式可变为|x-a|=1+，由|x-a|≥0，则1+≥0得，

分别作出的图像，

则关于x的方程f（x）=x+1有三个实根等价于的图像有三个交点，

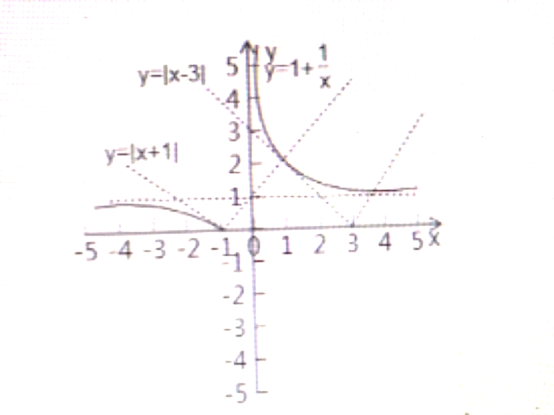
又函数的图像如图所示：

根据图象可知，当的图像有三个交点时，a＞3或者a＜-1，

故a的取值范围为a＞3或者a＜-1．