题目内容
【题目】如图,已知双曲线![]() 的右焦点为F,点A,B分别在C的两条渐近线上,
的右焦点为F,点A,B分别在C的两条渐近线上,![]() 轴,
轴,![]() ,
,![]() (O为坐标原点).
(O为坐标原点).
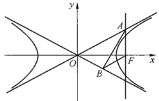
(1)求双曲线C的方程;
(2)过C上一点![]() 的直线
的直线![]() 与直线AF相交于点M,与直线
与直线AF相交于点M,与直线![]() 相交于点N.证明:当点P在C上移动时,
相交于点N.证明:当点P在C上移动时,![]() 恒为定值,并求此定值.
恒为定值,并求此定值.
【答案】(1)![]() (2)证明见解析;定值为
(2)证明见解析;定值为![]()
【解析】
(1)由直线![]() 和
和![]() 方程联立求出点
方程联立求出点![]() 的坐标,再根据
的坐标,再根据![]() ,即
,即![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)联立直线![]() 和直线
和直线![]() 的方程求出点
的方程求出点![]() ,联立直线
,联立直线![]() 和直线
和直线![]() 的方程求出点
的方程求出点![]() ,即可得到
,即可得到![]() 的表达式,再根据点
的表达式,再根据点![]() 在双曲线
在双曲线![]() 上,化简即可得到
上,化简即可得到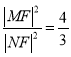 ,即命题得证.
,即命题得证.
(1)设![]() ,因为
,因为![]() ,所以
,所以![]() .
.
由题意可得,直线![]() 方程为
方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立解得
,联立解得![]() ,而直线
,而直线![]() 的方程为
的方程为![]() ,则
,则![]() ∴
∴![]()
又因为![]() ,所以
,所以![]() ,解得
,解得![]() ,故双曲线C的方程为
,故双曲线C的方程为![]()
(2)由(1)知![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]()
因为直线![]() 的方程为
的方程为![]() ,所以直线
,所以直线![]() 与
与![]() 的交点
的交点![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为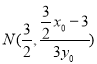 ,则
,则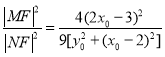 .
.
因为![]() 是C上一点,则
是C上一点,则![]() 代入上式得
代入上式得
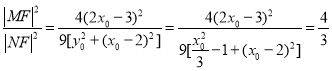 ,故所求定值为
,故所求定值为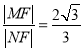 .
.

练习册系列答案
相关题目
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.