题目内容
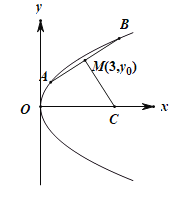
【题目】海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰在失事船的正南方向12海
里A处,如图. 现假设:①失事船的移动路径可视为抛物线![]() ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发![]() 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为![]() .
.
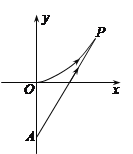
(1)当![]() 时,写出失事船所在位置P的纵坐标. 若此时两船恰好会合,求救援船速度的大小和方向;
时,写出失事船所在位置P的纵坐标. 若此时两船恰好会合,求救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
【答案】(1)arctan![]() 弧度;(2)25海里.
弧度;(2)25海里.
【解析】
(1)![]() 时,
时,![]() 的横坐标
的横坐标![]() ,代入抛物线方程
,代入抛物线方程![]() 中,得
中,得![]() 的纵坐标
的纵坐标![]() ,
,
由![]() ,得救援船速度的大小为
,得救援船速度的大小为![]() 海里/时,
海里/时,
由![]() ,得
,得![]() ,
,
故救援船速度的方向为北偏东![]() 弧度.
弧度.
(2)设救援船的时速为![]() 海里,经过小时追上失事船,
海里,经过小时追上失事船,
此时位置为![]() ,由
,由![]() ,
,
整理得![]() ,
,
因为![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
所以![]() ,即
,即![]() ,
,
因此,救援船的时速至少是![]() 海里才能追上失事船.
海里才能追上失事船.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
【题目】设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:
T(分钟) | 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返月老校区共用时间不超过120分钟的概率.