题目内容
设三棱锥P—ABC的顶点P在底面ABC内射影O(在△ABC内部,即过P作PO⊥底面ABC,交于O),且到三个侧面的距离相等,则O是△ABC的( )
| A.外心 | B.垂心 | C.内心 | D.重心 |
C
如图,设OD⊥AB于D,连结PD,则OD为PD在底面△ABC上的射影,∴PD⊥AB,∴AB⊥平面POD.
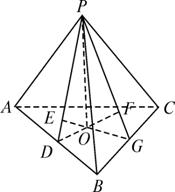
∴平面PAB⊥平面POD,且它们的交线为PD.作OE⊥PD于E,则OE⊥平面PAB,
∴OE即为点O到侧面PAB的距离.
同理可作出O到侧面PBC的垂线段OF.
∵OE=OF,∴Rt△PEO≌Rt△PFO.
∴∠DPO=∠GPO.
∴Rt△POD≌Rt△POG.∴OD=OG.
∴O为△ABC的内心

∴平面PAB⊥平面POD,且它们的交线为PD.作OE⊥PD于E,则OE⊥平面PAB,
∴OE即为点O到侧面PAB的距离.
同理可作出O到侧面PBC的垂线段OF.
∵OE=OF,∴Rt△PEO≌Rt△PFO.
∴∠DPO=∠GPO.
∴Rt△POD≌Rt△POG.∴OD=OG.
∴O为△ABC的内心

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
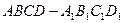 中,
中, ,点
,点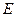 在
在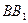 上且
上且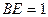 ,过点
,过点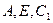 的平面截长方体,截面为
的平面截长方体,截面为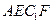 (
( 在
在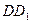 上).
上). 的长度; (2)求点C到截面
的长度; (2)求点C到截面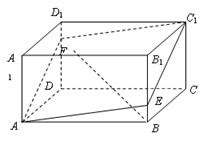
 过点
过点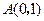 ,
,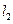 过点
过点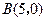 ,如果
,如果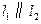 ,且
,且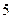 ,求
,求

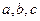 ,则长方体体对角线长为( )
,则长方体体对角线长为( )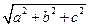
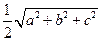
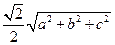
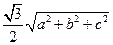
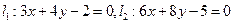 的距离等于( ).
的距离等于( ).

 ,且满足
,且满足 则
则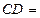 .
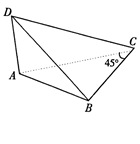
.

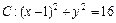 上一动点,则点P到直线
上一动点,则点P到直线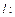
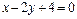 的最远距离是( ).
的最远距离是( ).