题目内容
17.“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:| 男性 | 女性 | 合计 | |
| 反感 | a=10 | b= | |
| 不反感 | c= | d=8 | |
| 合计 | 30 |
(1)请将上面的2×2列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
参考数据和公式:
2×2列联表K2公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,K2的临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据在全部30人中随机抽取1人抽到中国式过马路的概率,做出中国式过马路的人数,进而做出男生的人数,填好表格.再根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明反感“中国式过马路”与性别是否有关.
(2)反感“中国式过马路”的人数为X的可能取值为0,1,2,通过列举得到事件数,分别计算出它们的概率,最后利用列出分布列,求出期望即可.
解答 解:(1)
| 男性 | 女性 | 合计 | |
| 反感 | 10 | 6 | 16 |
| 不反感 | 6 | 8 | 14 |
| 合计 | 16 | 14 | 30 |
设H0:反感“中国式过马路”与性别与否无关
由已知数据得:K2=$\frac{30(10×8-6×6)^{2}}{16×14×16×14}$≈1.158<3.841,
所以,没有充足的理由认为反感“中国式过马路”与性别有关.…(6分)
(2)X的可能取值为0,1,2.
P(X=0)=$\frac{{C}_{8}^{2}}{{C}_{14}^{2}}$=$\frac{4}{13}$,P(X=1)=$\frac{{C}_{6}^{1}{C}_{8}^{1}}{{C}_{14}^{2}}$=$\frac{48}{91}$,P(X=2)=$\frac{{C}_{6}^{2}}{{C}_{14}^{2}}$=$\frac{15}{91}$ …(9分)
所以X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{4}{13}$ | $\frac{48}{91}$ | $\frac{15}{91}$ |
点评 本题是一个统计综合题,包含独立性检验、离散型随机变量的期望与方差和概率,本题通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.在△ABC中,若C=$\frac{π}{4}$,a=6,B=$\frac{π}{6}$,则ab等于( )
| A. | 36$\sqrt{3}$+36 | B. | 6$\sqrt{3}$+6 | C. | 3$\sqrt{6}-3\sqrt{2}$ | D. | 18$\sqrt{6}-18\sqrt{2}$ |
9.随机变量X的概率分布如下,则P(X≤1)=0.4.
| X | 0 | 1 | 2 | 3 |
| P | 0.3 | m | 0.5 | 0.1 |
7.某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取2人,求成绩名次在1~50名恰有1名的学生的概率.
附:P(K2≥3.841=0.05)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取2人,求成绩名次在1~50名恰有1名的学生的概率.
附:P(K2≥3.841=0.05)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
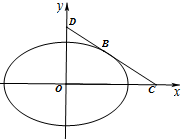 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.