题目内容
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,整理得:
,整理得:![]() ,可得
,可得![]() ,
,![]() ,
,![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列;(2)由(1)可知:
的等差数列;(2)由(1)可知:![]() ,利用“错位相减法”即可求得
,利用“错位相减法”即可求得![]() ;(3)由
;(3)由![]() 得
得![]() ,整理得:
,整理得:![]() ,当
,当![]() 为奇数时,
为奇数时,![]() ;当
;当![]() 为偶数时,
为偶数时,![]() ,由
,由![]() 为非零整数,即可求得
为非零整数,即可求得![]() .
.
试题解析:(1)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() (常数),
(常数),
又![]() ,∴
,∴![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() .
.
(2)![]() ,
,
![]() ,
,![]() ,
,
相减得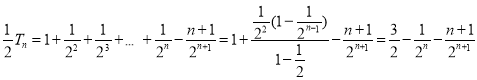 ,
,
∴![]() .
.
(2)由![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ,∴
,∴![]() ;
;
当![]() 为偶数时,
为偶数时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() 为非零整数,∴
为非零整数,∴![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目