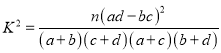题目内容
【题目】7人站成一排.（写出必要的过程，结果用数字作答）
（1）甲、乙两人相邻的排法有多少种？
（2）甲、乙两人不相邻的排法有多少种？
（3）甲、乙、丙三人两两不相邻的排法有多少种？
（4）甲、乙、丙三人至多两人不相邻的排法有多少种？
【答案】（1）1440（2）3600（3）1440（4）4320
【解析】试题分析：本题主要考查排列问题中的特殊解题方法，解决“相邻”问题用“捆绑法”，利用整体思想，解题的思路是先整体、再局部；解决“不相邻”问题用“插空法”，也就是先排可以相邻的元素，再将要求不相邻的元素插入空中；用“间接法”解题，先不用考虑限制条件，计算出排列的总数，再减去不符合要求的排列数.
试题解析：（1）（捆绑法）将甲、乙两人“捆绑”为一个元素，与其余5人全排列，共有
种排法，甲、乙两人可交换位置，有
种排法，故共有
（种）排法.
（2）方法一（间接法）7人任意排列，有
种排法，甲、乙两人相邻的排法有
种，故甲、乙不相邻的排法有
（种）.
方法二（插空法）将其余5人全排列，有
种排法，5人之间及两端共有6个位置，任选2个排甲、乙两人，有
种排法，故共有
（种）排法.
（3）（插空法）将其余4人拍好，有
种排法，将甲、乙、丙插入5个空中，有
种排法.故共有
（种）排法.
（4）（间接法）
.
练习册系列答案
相关题目
【题目】为了研究某种微生物的生长规律，需要了解环境温度
（
）对该微生物的活性指标
的影响，某实验小组设计了一组实验，并得到如表的实验数据：
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
（Ⅰ）由表中数据判断关于
的关系较符合
还是
，并求关于的回归方程（
，
取整数）；
（Ⅱ）根据（Ⅰ）中的结果分析：若要求该种微生物的活性指标不能低于
，则环境温度应不得高于多少？
附：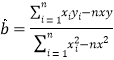
，
