题目内容
【题目】若函数![]() 存在极值,且这些极值的和不小于
存在极值,且这些极值的和不小于![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】f(x)=ax﹣x2﹣lnx,x∈(0,+∞),
则f′(x)=a﹣2x﹣![]() ,
,
∵函数f(x)存在极值,∴f′(x)=0在(0,+∞)上有根,
即2x2﹣ax+1=0在(0,+∞)上有根,∴△=a2﹣8≥0,
显然当△=0时,F(x)无极值,不合题意;
∴方程必有两个不等正根,记方程2x2﹣ax+1=0的两根为x1,x2,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
f(x1),f(x2)是函数F(x)的两个极值,
由题意得,f(x1)+f(x2)=a(x1+x2)﹣(x12+x22)﹣(lnx1+lnx2)
=![]() ﹣
﹣![]() +1﹣ln
+1﹣ln![]()
![]() 4﹣ln
4﹣ln![]() ,
,
化简解得,a2![]() 12,满足△>0,
12,满足△>0,
又x1+x2=![]() >0,即a>0,
>0,即a>0,
∴a的取值范围是[![]() ,+∞),
,+∞),
故答案为:C。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在高中学习过程中,同学们常这样说:“如果你的物理成绩好,那么你的数学学习就不会有什么大问题.”某班针对“高中物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系,如表为该班随机抽取6名学生在一次考试中的物理和数学成绩:
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩(x) | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求数学成绩y对物理成绩x的线性回归方程;
(2)该班某同学的物理成绩100分,预测他的数学成绩.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
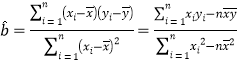 ,
,![]()
参考数据:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.