题目内容
【题目】选修4-5：不等式选讲
设函数f(x)＝x2－x－15，且|x－a|<1，
(1)解不等式
；
(2)求证：|f(x)－f(a)|<2(|a|＋1)．
【答案】（1）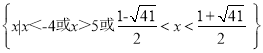
（2）见解析
【解析】试题分析：（1）先根据绝对值定义将不等式转化为两个一元二次不等式，分别求解，最后求它们的并集（2）作差f(x)－f(a)因式分解得(x－a)(x＋a－1)，根据条件|x－a|<1以及绝对值三角不等式放缩可得结论
试题解析：(1)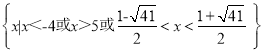 
(2)∵|x－a|<1，
∴|f(x)－f(a)|＝|(x2－x-15)－(a2－a-15)|
＝|(x－a)(x＋a－1)|
＝|x－a|·|x＋a－1|<1·|x＋a－1|
＝|x－a＋2a－1|≤|x－a|＋|2a－1|<1＋|2a－1|≤1＋|2a|＋1
＝2(|a|＋1)，
即|f(x)－f(a)|<2(|a|＋1)．
练习册系列答案
相关题目
